הקדמה:
אחת השאלות המרתקות במדע בן ימינו קשורה בזיקה שבין סדר לאי סדר בטבע. המערכות הפיסיקליות בטבע כפופות לעקרון האנטרופיה, הקובע שהאי סדר נמצא בעליה מתמדת וכי בסופו של דבר כל מבני החומר עתידים להתפורר ולהתפרק, ובכך יקיץ הקץ על היקום כולו. אבל בשנים האחרונות התגבשה השקפה אחרת, לפיה אין לראות באי סדר סוף פסוק אלא להיפך – מקור אפשרי של יצירת סדר ואירגון.
ים גלי הוא דוגמה נאה למערכת אקראית חסרת שיווי משקל. גלים בגדלים שונים נעים בכיוונים שונים, מתנגשים זה בזה ומבטלים או מעצימים זה את זה באורה אקראי לחלוטין. אבל, במקרים נדירים מאוד קורה שהשיאים של קבוצת גלים אחת מתחברים עם השיאים של קבוצת גלים אחרת, ואז, ללא כל התראה מוקדמת ובאופן מפתיע ביותר, נוצר ממצב זה של אקראיות מוחלטת מבנה מסודר להפליא: “גל אימה״ המתנשא לגובה של 25 מטר והמסוגל להטביע תוך שניות ספינות ואוניות.
אם תרצו, גל האימה, מעצם העובדה שהוא תוצאה ייחודית וחד פעמית שלא ניתנת לחיזוי ולניבוי, מבטל את האבחנה המסורתית שלפיה התופעות הפיסיקליות מתאפיינות בכך שהן חזויות והדירות – כלומר חוזרות על עצמן – בעוד היצירה האמנותית היא תוצאה של אקט ייחודי והד פעמי. גל האימה הוא ייחודי וחד פעמי כמו שיר, כמו ציור, כמו סיפור.
פרופ׳ הנרי אטלן הוא פרופסור לביופיסיקה באוניברסיטה העברית ומנהל המחלקה לביופיסיקה רפואית ורפואה גרעינית בבית החולים הדסה בירושלים.
פרופ’ אטלן חוקר את הביולוגיה של התא ושל ההזדקנות, ובמקביל לכך מנהל רומן ממושך עם הפילוסופיה של המדע. הוא פירסם שלושה ספרים על מערכות בעלות כושר אירגון עצמי, על תיאוריות של מורכבות ועל מדע ואתיקה.
פרופ’ אטלן הוא דמות ידועה ומוכרת בצרפת בחוגי המדע, האינטליגנציה והשלטון.

שאלת היחס בין האמנות והמדע שבה ועולה על סדר היום שלנו, ורצוי אולי לחשוב למה. אני משער שקיימת בנו שאיפה לאיחוד הרגש עם השכל והאמת ועם היפה, ברוח האידיאל האפלטוני של איחוד האמת, היפה והטוב. אלא ששאיפה עתיקת יומין זו נמצאת בסתירה עם המציאות, ועקב כך נוצר מתח מסוים. ברור שהפרקטיקה המדעית שונה מהפרקטיקה האמנותית מכל מיני בחינות, כשם שברור שהחיפוש אחר האמת שונה מהחיפוש אחר היופי. לכאורה, האמת היא מה שקיים, ומדעי הטבע נתפסים כמאמץ לגלות את העובדות הקשורות בקיים. קשר זה הוא כה חזק, עד כי מדענים אחדים סבורים שבמדע אין יצירתיות, כיוון שהוא לא יוצר דבר, אלא רק מגלה את הקיים. לעומת המדע, האמנות היא סמל ליצירתיות, כי היא מבוססת על דמיון, והדמיון כידוע איננו מוגבל על ידי הקיים. אבל במבט שני נראה כי אבחנה קטגורית זו בין המדע לאמנות איננה נכונה. בכל אחד מהם יש משהו מהשני, וכנראה גם קיימת ביניהם השפעת גומלין לא ישירה. על ההשפעה הלא ישירה הזאת אפשר לעמוד מכך שגם במדעי הטבע החיפוש אחר האמת אינו עיקרון אבסולוטי. גם הוא מושפע מרוח הזמן. המערכת הניסויית, ויותר ממנה המערכת המושגית (פיענוח תוצאות הניסוי והסקת מסקנות מהן), אינן ניטרליות והן נתונות להשפעות הסביבה. לדוגמה אביא את מושג התוכנה הגנטית, הקשורה ישירות לנושא של הרצאה זו על הסדר והאי סדר בביולוגיה.
שאלת ההתארגנות העצמית
בשנות השישים פותחו כמה תגליות שהיוו את הבסיס לביולוגיה המולקולרית המודרנית. הן היו כל כך חשובות, עד כי היה צורך למצוא מערכת תיאורטית מושגית שתסביר אותן. באותה תקופה, בתחום אחר לחלוטין, ובמידה רבה בצורה אקראית, התפתח מושג30 התוכנה במדעי המחשב. מושג זה, שכאילו נפל מן השמיים לידי הביולוגים, איפשר להם להסביר בצורה אלגנטית וכוללנית רבים מממצאיהם ומתגליותיהם בתחום הביולוגיה המולקולרית. כך נוצר המושג תוכנה גנטית. זאת אומרת, מושג מרוח התקופה השפיע על המחקר בביולוגיה.

באמנות, חוויית היופי נובעת מהצורה. במדע לא הצורה חשובה אלא התוכן

אלא שהמושג החדש נחשף מיד לביקורת. הוא היה מטאפורי מדי, ולפיכך לא די מדויק ולא די מדעי. מאחר שכך, החלו חוקרים אחדים לחפש מושג אחר מתחום החיים, שהרי כשמדברים על תוכנת מחשב, מניחים קיומו של מתכנת שהכניס בתוכנית כוונה וכיווניות, ואילו האבולוציה של בעלי החיים לא מתנהלת על פי כוונה ומגמה של מישהו, אלא אם כן מאמינים בהכוונה אלוהית. אבל עירוב האלוהים באבולוציה ממילא לא פותר דבר, כיוון שאיננו יודעים את כוונותיו ואיננו מכירים את שפת התיכנות שלו. הואיל וכך, ניסו כמה חוקרים לנסח עקרונות אחרים, המבוססים על אירגון עצמי, זאת אומרת, עקרונות שלפיהם ניתן יהיה להסביר או להבין מנגנונים שבאמצעותם חומר יכול להתארגן מעצמו בלי להיעזר בתוכנה חיצונית. מיד הובאה הוכחה, על ידי רוס אשבי (Ross Ashby), שאירגון עצמי הוא בלתי אפשרי. מדוע? כי אם מגדירים אירגון כחוק שלפיו פועלת המערכת, השינוי בחוק הוא מה שמעניין אותנו כשמדובר בהתארגנות. ואם כך, יש שתי אפשרויות: אם מה שמשנה את החוק בא מבחוץ, אזי ברור שלא מדובר בהתארגנות עצמית אלא בהשפעה מבחוץ; ואם מה שמשנה את החוק בא מבפנים, מחפשים מיד מהו החוק שעל פיו קורה השינוי, ומוצאים שיש חוק שמגדיר איך קורה השינוי של החוק. חוק-על זה, המגדיר כמובן את האירגון של המערכת הזאת, הוא עצמו אינו משתנה, ולכן אי אפשר לדבר על התארגנות. אם הוא ישתנה, נחפש חוק על-על, וכן הלאה. אשבי חשב אם כן, שאירגון עצמי אינו קיים, כי השינוי באירגון, כלומר ההתארגנות, אינו יכול לבוא מבפנים, אלא רק מבחוץ. אבל במבט שני אפשר להבין כי את מה שיכול לבוא מבחוץ ניתן לחלק לשני סוגים: סוג אחד הוא תוכנה, זאת אומרת הוראות חיצוניות שמשנות את האירגון, ואז באמת אין סיבה לדבר על התארגנות עצמית. הסוג השני יכול להיות לא הוראות, אלא סתם רעש שבא מבחוץ, גירויים אקראיים. ההשקפה הקלסית התייחסה לגירויים אקראיים הפועלים על מערכת מאורגנת כאל הפרעות, דהיינו ראתה בהם גירויים שליליים שיכולים לגרום לחיסול האירגון במערכת. אבל יש הוכחות לכך כי בתנאים מסוימים גירויים אקראיים יכולים לגרום לשינויים באירגון המשפרים את יעילותה של המערכת. אפשר כמובן לשאול, ייעול על פי איזה31 קריטריון. התשובה היא – על פי קריטריון ההסתגלות. כלומר אותו קריטריון בסיסי העומד ביסוד החיים והמאפשר לבעלי החיים להסתגל למצב החדש ולהגיב לכל מיני גירויים לא צפויים, על ידי שינוי האירגון שלו. מאז, ובעזרת כמה שיטות מתמטיות ופיסיקליות, הלך והתברר כי התארגנות עצמית היא לא רק אפשרית, אלא גם קיימת בפועל. ומה שמעניין לא פחות, התארגות עצמית קיימת לא רק בביולוגיה כי אם גם בפיסיקה ובבינה מלאכותית.
סדר מאי סדר
כדי להמחיש את הזיקה בין חוסר סדר לסדר אביא דוגמה מהחומר החי, הביולוגי, הנמצא באמצע הדרך בין הגביש והעשן1 . הגביש הוא מופת של אירגון רגולרי. יש לו מבנה שחוזר על עצמו, ודבר זה יוצר תחושה של יופי מסוים, הקשור לסימטריות ולמחזוריות. בקצה שני נמצא העשן המייצג את האי סדר המוחלט. זמן רב נחשב הגביש למודל הפיסיקלי לאירגון ביולוגי. היום ברור שהמודל הזה איננו טוב מכל מיני בחינות. גם הגז או העשן, שהגיעו לאנטרופיה מקסימלית, אינם מודל טוב למצב החי. האירגון הביולוגי נמצא במקום כלשהו באמצע, כי יש קשר הדוק בין האי סדר ובין ההשתנות המאפשרת הסתגלות. מאחר שכך, אפשר לראות שאין סתירה גמורה, כפי שהיה נדמה, בין אקראיות ובין אירגון. להיפך, בתנאים מסוימים האקראיות יכולה להיות תנאי להתארגנות עצמית, המאפשרת לבעלי החיים להסתגל לדברים חדשים ובלתי צפויים. אם כן, בחרתי בכוונה בדוגמה מופשטת, כדי שיהיה אפשר להחיל אותה על כל מיני מצבים ותחומים אחרים. מדובר ברשת בצורת סריג, אשר בכל אחד מקשריו (רישום 1) נמצאת יחידה. כל יחידה מקבלת אות משני שכנים ושולחת אות לשני השכנים האחרים שלה. האות הוא בינארי (ספרתי), זאת אומרת הוא יכול להיות אפס או אחד. היחידה מבצעת חישוב על שני אותות אלו של מידע ומוציאה תוצאה, הכתובה אף היא בשפה בינארית. למשל, רישום 2 הוא דוגמה של חישוב כזה: האות שבא מצד אחד יכול להיות אפס או אחד, והאות שבא מצד שני נם הוא יכול להיות אפס או אחד. אם שניהם אפס, התוצאה היא אחד, אם הראשון הוא אפס והשני אחד התוצאה היא אחד וכו׳. אפשר להגדיר פעולה זאת כחוק חישוב, וקל לראות שקיימות 16 אפשרויות לביצוע חישוב כזה (רישום 3). במלים אחרות, אפשר לצייר 16 טבלאות כאלו, שכל אחת מגדירה חוק חישוב אחר, דהיינו כל אחת מגדירה צורה אחת מיוחדת לה לחשב שני שדרים. אפשר כמובן להגדיל את הרשת למאות יחידות ולהפעיל בתוכה באופן אקראי את חוקי החישוב, כמתואר ברישום 4. כל מספר בטבלה מייצג אחד מ-16 חוקי החישוב החלים על יחידה מסוימת בתוך הרשת. האקראיות מתבטאת בהקצאת חוקי החישוב השונים ליחידות השונות. גם המצב ההתחלתי של הרשת, זאת אומרת המצב ההתחלתי של כל יחידה, (אם הוא אפס או אחד), נעשה באקראי. כתוצאה מכך, מקבל כמובן המבנה כולו אופי אקראי. עכשיו נותנים לרשת לפעול, כלומר מאפשרים לכל יחידה ויחידה לחשב את המצב הבא שלה על סמך האותות שקיבלה וחוק החישוב שלה; התוצאה שהתקבלה נהפכת לשדר הנשלח ליחידות שכנות, אלו 32מחשבות את מצבן על פי המידע שקיבלו ושולחות את התוצאה ליחידות שכנות, וכן הלאה. אחרי זמן מה יתגבש ברשת אירגון יציב כפי שמתואר ברישום 5. כל מקום המצוין באות s (stable) מראה שהיחידה היא יציבה, כלומר, היא לא משנה את מצבה בין אם השדר היה אפס ובין אם היה אחד. כל היחידות האחרות המצוינות באות p (periodic) עוברות שינוי מחזורי – מצבה של כל יחידה משתנה אחרי סדרה קצרה של מצבי אפס ואחד וחוזרת למצבה הראשון. לכן, אם מתחילים מהמבנה המיקרוסקופי המתואר ברישום 4, שבחלקו הוא מבנה אקראי, מגיעים בסופו של דבר למצב היציב, והמצב היציב הזה הוא בעל מבנה במרחב (שמתבטא בחלוקה לתת רשתות) ובזמן (שמתבטא בתכונות מחזוריות בכמה מהתת רשתות האלה). חשוב לציין שהמבנה הזה מופיע ברמה של מאקרו (רישום 5), כלומר ברמה יותר כוללנית מהרשת ההתחלתית. את הדוגמה הזאת אפשר כאמור להחיל על מצבים שונים. למשל, במקום היחידות הבינאריות אפשר לשים יחידות יותר מתוחכמות דוגמת הנוירונים במוח. לכן הסריג הזה יכול להיות מודל, פשטני אמנם, לתכונות של התארגנות עצמית במוח.
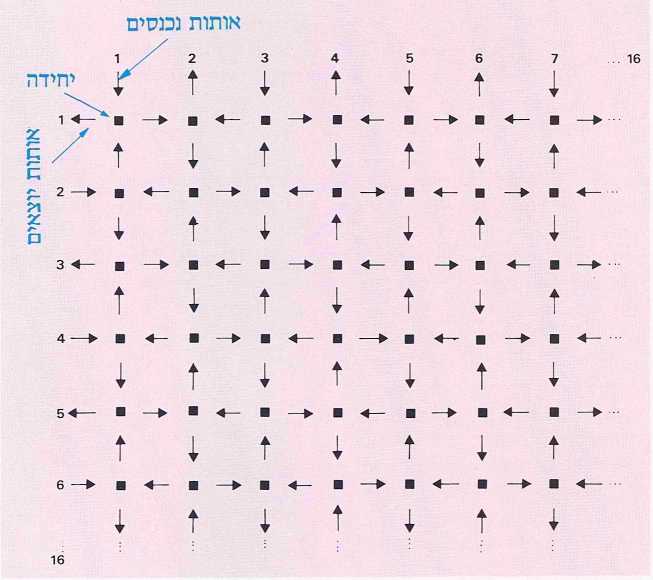
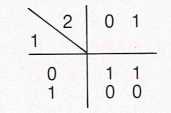
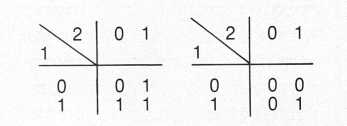


במצבים מסוימים האקראיות יכולה להיות תנאי להופעת הסדר
ממחזוריות ליציבות
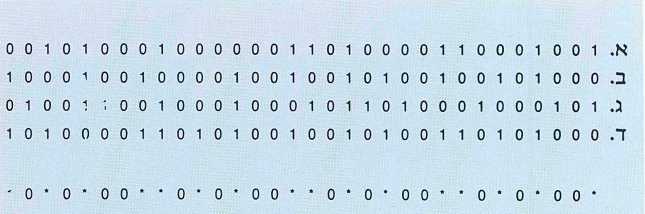
תופעת ההתארגנות העצמית קיימת בתחומים שונים בפיסיקה ובכימיה, ובעצם היא ידועה מאוד. מה שפחות ידוע הוא שניתן לפענח אותה לא רק כיצירה של אירגון במרחב ובזמן, אלא גם כיצירה של אירגון פונקציונלי. למשל, במקום לתת לרשת להישאר במצב המנוחה שהיא הגיעה אליו אחרי זמן מה, אפשר לעורר מחדש את אחת היחידות, הפעם באמצעות אותות בינאריים מבחוץ. עוקבים אחרי השפעתה של שרשרת האותות הבינאריים האלה על אחת היחידות ברשת, ודרכה על מצבה של יחידה אחרת רחוקה ממנה, ובודקים את אופי ההשפעה. כלומר, מחפשים אם יש שרשרות אשר בהיכנסן ליחידה הראשונה הן גורמות לשדר היוצא ממנה לשנות את מצבה של היחידה השנייה.33 במיוחד מחפשים שינוי ממצב מחזורי למצב יציב. אם יש שרשרות כאלה, אנחנו אומרים שהרשת מכירה אותן. על שרשרות אחרות, שאינן משנות את מצבה של היחידה השנייה, אנחנו אומרים שהרשת לא מכירה אותן. לכן שתי היחידות האלו, זו שקלטה את שרשרת האותות מבחוץ וזו ששינתה את מצבה (מ-p ל-s) בעקבות השדר שקיבלה מהיחידה הראשונה, משמשות ככניסה וכיציאה למערכת של זיהוי צורות (Pattern Recognition System). רישום 6 מראה ארבע שרשרות של אותות חיצוניים. מתברר שבניסיון מסוג שתיארתי עכשיו, המערכת ״הכירה״ (כלומר הרשת שינתה מצב אחת מיחידותיה מ-p ל-s) את השרשרת הראשונה, השנייה וגם הרביעית, אבל לא את השלישית (ג). התשובה על השאלה מהו הקריטריון המאפשר למערכת להכיר שרשרת מסוימת, טמונה בשרשרת התחתונה בעלת הכוכביות. פירושו של כוכב הוא כי בנקודה המצוינת על ידו, האות הבינארי יכול להיות אפס או אחד בלי שהדבר ישנה את יכולתה של הרשת להכיר את השרשרת. אך כדי ששרשרת מסוימת תוכר, היא צריכה להתאים לאותות האחרים, שאינם מסומנים בכוכביות. מה שחשוב לענייננו הוא שאיש לא תיכנת את הקריטריון הזה, הוא פרי התארגנות עצמית.
בהסתגלות של בעל חיים לסביבה שלו אפשר לראות יסוד של יצירתיות
פירוש הדבר שתהליך ההתארגנות לא רק מסוגל להוציא צורות מאקרוסקופיות על בסיס מבנה מיקרוסקופי (דהיינו, מטבלת חוקי החישוב של רישום 4 יכולים לצאת המבנים היציבים והמחזוריים ברישום 5) שיש בו חוקיות וגם אקראיות, הוא גם יכול להוציא פונקציות כגון פונקצית זיהוי של צורות (שרשרות) מסוימות, בעוד קריטריון הזיהוי אינו מתוכנת, אלא נובע מהאירגון העצמי.
השינוי הבלתי צפוי
דוגמה זו היא רק אחת מני רבות. המסקנה היא שכאשר חושבים על סדר בעולם הטבעי, לא מוכרחים לחשוב רק במושגים של סימטריה. באותה מידה אפשר לחשוב במושגים של סימטריה שבורה, משהו שבין הגביש והעשן, כך שתיכלל בהם גם ההשפעה האפשרית של האקראיות. מחשבה זו היא מושכת מאוד, כי אנחנו יכולים לראות איך בעל חיים, אפילו ברמה של תא, מסתגל לסביבה שלו, ויש בהסתגלות זו סוג של פעולה שאפשר למצוא בה איזשהו יסוד של יצירתיות. כי התא המסתגל לשינוי בסביבה אינו רק, כפי שנוטים לחשוב, תוכנת מחשב שמניבה להוראה חדשה, אלא גם מערכת שמגיבה לגירוי אקראי על ידי שינוי יצירתי באירגון שלה. ולמה יצירתי? כי שום מדען ושום צופה חיצוני לא מסוגלים לצפות מראש את השינוי על כל פרטיו.
עניין זה מחזיר אותנו לשאלת היצירתיות שהתחלנו בה, אבל כמובן ברמה אחרת, לא היצירתיות שאנחנו מוצאים בטבע, אלא היצירתיות האמנותית או המדעית. כאן המקום לשאול מניין התחושה האסתטית שאנחנו מרגישים בה נוכח מעשה יצירה, מול דבר שהוא חדש ובכל זאת מוכר לנו. התכונה הזאת, המאפיינת כל תהליך של לימוד מהניסיון, מכילה לכאורה יסוד של פרדוקס, כי ניתן להוכיח לכאורה שאי אפשר ללמוד שום דבר חדש, על פי אותו ההיגיון ששימש את רוס אשבי כשדיבר על חוסר האפשרות של אירגון עצמי. שהרי אם מציגים לי משהו חדש לחלוטין אינני מסוגל להכירו, ולכן אני לא יכול ללמוד אותו. ואם מה שמציגים לי איננו חדש, משמע שהוא מוכר וידוע לי, ועל כן גם במקרה זה אינני לומד ממנו דבר. איך יוצאים מפרדוקס זה? איך אפשר לקבל משהו חדש ממשהו מוכר?
ובכן, קודם כל צריך להבין שאנחנו לא רק קולטים מידע מבחוץ, אלא גם משליכים צורות, דימויים ומושגים, הקיימים במערכת הקוגניטיבית שלנו, על העולם החיצוני. כשיש התאמה כלשהי בין הצורות שאנחנו משליכים ובין הגירויים שבאים מבחוץ, נוצרת אצלנו תחושה של היכרות שאפשר לתארה כתחושה של סיפוק. התחושה הזאת יכולה לעלות לא רק כשההתאמה שלמה, אלא גם כשהיא חלקית, כי אז אנחנו משלימים את החסר. לכן אולי אפשר לייחס את תחושת הסיפוק הנובעת מתהליך ההיכרות למה שקוראים בפסיכואנליזה הדחף לדעת. ואני מתכוון לשתי משמעויותיו של הפועל לדעת בעברית – גם האינטלקטואלית-קוגניטיבית וגם המינית. עם זאת, צריך להבדיל בין סוגי הידיעה השונים, ובייחוד לראות כסוג נפרד את סוג הידיעה המדעי, שהתפתח בהיסטוריה באופן שונה מסוגי הידיעה האחרים, הלא מדעיים, ואשר הצלחתו תלויה בצורתו המיוחדת. הדרך הכי פשוטה אולי להבדיל בין כללי המשחק34 המדעי ובין כללי המשחק האמנותי, היא להסתכל בשימוש השונה שהם עושים בשפה. במדע אנחנו שואפים לשפה שקופה, מדויקת וחד משמעית ככל האפשר. השפה הלוגית-מתמטית היא האידיאל של השאיפה הזאת. בפרקטיקה האמנותית וגם בפרקטיקות אחרות, המיסטיות למשל, כיוון החיפוש הוא הפוך: בתחומים האלה אנחנו מניחים שהמציאות הנסתרת שוכנת מעבר לשפה, ועל כן השפה לא יכולה לבטא מה שאנחנו רוצים להביע. השפה יכולה רק להציע או לומר משהו ברמז, בעקיפין, ולכן היא מטאפורית מאוד. לפיכך גם היחס בין הצורה והתוכן משתנה. בעבודה אמנותית המרכיב החשוב ביותר הוא הצורה. התוכן לא כל כך חשוב. אפשר לעשות ציור אמנותי נפלא על תפוח. התוכן הוא התפוח, אבל מה שמעורר את חוויית היופי הוא כמובן הצורה. גם בשיר הצורה חשובה מהתוכן. במדע מצב הדברים הפוך. הסגנון לא כל כך חשוב, מה שחשוב באמת הוא התוכן, ההוכחה.


כמובן, יש צורות שונות של הוכחה. יש הוכחות אלגנטיות שמעוררות תחושה אסתטית עמוקה, אבל לא זה הדבר הקובע בסופו של דבר, שהרי יש תיאוריות מאוד אסתטיות, אבל לא נכונות. נדמה לי שהשוני בשפה מייצג את ההבדל העיקרי בין כללי המשחק הפועלים באמנות ובמיסטיקה, מצד אחד, ובמדע מצד שני. מעניין לציין שבשפת היומיום שלנו אנחנו עושים שימוש מעורב בשתי השפות גם יחד, אבל כשבאים לנסח את הדברים באופן תיאורטי, יש לשמור כל שפה לתחומה היא. אין מקום לחבר תיאוריה מדעית מתורה מיסטית או אמנותית, ולהיפך. על כל שפה לשמור על ייחודה אך בלי לזלזל ברעותה. ■35
כשם ספרו של הנרי אטלן: ENTRE LE CRISTAL ET LA FUMEE (בין הגביש והעשן), H. ATLAN, PARIS, SEUIL, 1979 ↩







