הקדמה:
ב-1854 הופיעה ב״טיימס״ של לונדון כתבה על הפצועים הבריטים במצור סבסטופול. הם היו מוטלים בשדה ללא טיפול, וגם מי שזכו להגיע בדרך הים לבית-חולים, מתו שם ברובם ממחלות. מצב הפצועים הצרפתים היה טוב יותר, כי חיל-המשלוח הצרפתי במלחמת קרים כלל גם 50 אחיות-נזירות. דעת הקהל בבריטניה נזדעזעה. שר-המלחמה שלח לחזית את פלורנס נייטינגל הצעירה, בת-אצילים שהתמסרה מנעוריה לקידום הסיעוד הרפואי, כשהיא מצוידת בסמכויות ישירות ממנו ובקרן תרומות שארגן ה״טיימס״. אי-תלותה בצבא והיותה אישה עוררו התנגדות נמרצת בפיקוד הצבאי. מכשול נוסף היה הביורוקרטיה הקיצונית: האפסנאי הראשי לא הסכים לספק שום סדין מהסדינים שהתחילו להגיע ושהיו דרושים בדחיפות בבית-החולים, עד שכל המשלוח של 27 אלף סדינים יגיע מבריטניה בשלמותו, וייבדק ויאושר בידי המפקח.
על אף הקשיים, הגיעה נייטינגל להישגים מרשימים. במאמץ ארגוני והדרכתי בלתי-נלאה, בהקפדה על היגיינה ועל הרתחת כבסים ובטיפול מסור בפצועים הצליחה להוריד את רמת התמותה מ-42 אחוזים מן הנקלטים בבית-החולים לפני בואה, ל-2.2 אחוזים. לאחר המלחמה נעשתה ״הגברת עם הפנס״ (כך נקראה בגלל סיוריה הליליים בחדרי הפצועים), דמות נערצת באנגליה ובאירופה כולה. המלכה ויקטוריה וראש-הממשלה לורד פלמרסטון התחילו להקשיב לרעיונותיה ולהצעותיה, אשר הביאו בסופו של דבר לירידת התמותה השנתית בקרב החיילים הבריטים בשירות פעיל מ-69/1,000 ל-18/1,000.
נאמנה לגישתה היסודית והשיטתית, עשתה נייטינגל שימוש במחקר סטטיסטי לביסוס השגותיה והצעותיה. מאחר שידעה שמקבלי ההחלטות אינם רגילים לחשוב במונחי כמות, פיתחה שיטות גרפיות מקוריות להמחשת הנתונים שבידיה. שיטוח אלה נמצאות בשימוש גם כיום.
נייטינגל למדה את עקרונות הסטטיסטיקה החברתית מן הבלגי קֶטֶלֶה, שספרו פיסיקה חברתית הופיע ב-1836. קטלה סבר, שבחברות אנושיות שולטים חוקים ברורים, הדומים לחוקים השולטים בעולם החומר. למשל, אי-אפשר לדעת אם פלוני ישפוך דם, יזייף או ירעיל בשנה הבאה; אבל אפשר לומר במידה רבה של ביטחון, מה יהיה מספרם הכולל של מעשי החבלה, הזיוף וההרעלה באוכלוסיית צרפת בשנה. בדומה לכך, אין לדעת אם פצוע פלוני יחלים עקב הטיפול בבית-החולים, אבל אפשר לחזות מראש את מספרם הכולל של המחלימים, של הנפטרים ושל מי שייעשו נכים מקרב הנקלטים בבית-החולים הצבאי מדי חודש בחודשו. אפשר גם לבחון את השפעתן של שיטות סיעודיות שונות על נתונים אלה.
לא כולם הסכימו עם רעיונותיו של קטלה ועם טיעוניה הסטטיסטיים של נייטינגל. הפילוסוף הבריטי ג׳ון סטיוארט מיל הדגיש את אי האפשרות ללמוד חוקים כלליים מתוך מקרים פרטיים רבים ככל שיהיו. הסופר צ׳ארלס דיקנס לגלג על השימוש בממוצעים ותיאר חיילים בריטים הקופאים מקור בלילה, משום שסופקו להם בגדים מתאימים לטמפרטורה ממוצעת שנתית של 20 מעלות, השוררת באזור.
העובדה שמאפיינים מסוימים של אוכלוסיות גדולות יציבים בזמן ומאפשרים ניבוי ובחינת השפעות, היא גם כיום כלי ניתוח והיסק רב-עוצמה, ובה בעת היא מהווה סוגיה תיאורטית שבירורה עודנו בעיצומו.
איורים: אבנר כץ
קוביות וקיצבאות
המושגים מרחב, זמן, מספר, מידה, סיבה, תכלית, אטום, יקום ורבים אחרים מן המושגים שבאמצעותם אנו תופסים את המציאות, היו מוכרים כבר בזמן העתיק. לא כן סיכוי והסתברות. מושגים אלה לא היו ידועים במובנם הנוכחי בתרבות המערבית עד המאה ה־17. הם נרמזים בעולם העתיק רק בכתבים הודיים ובתלמוד. אין ספק, שהרקע התצפיתי למושג ההסתברות ההבחנה בשכיחויות יציבות של מאורעות מקריים – היה מוכר בחברה האנושית עוד בימי־קדם. בקברים מצריים עתיקים נמצאו קוביות־משחק עשויות שנהב. בבדיקות שנערכו נמצא, שהן סימטריות מאוד, כלומר שהשכיחות היחסית של שש התוצאות האפשריות כמעט זהה.
אנשים השתתפו בהימורים ובמשחקי־מזל, והיו בוודאי מי שהיטיבו להמר מאחרים: הם הכירו מניסיונם את השכיחויות היחסיות. הטלת גורל נזכרת במקרא. עכן, ששלח ידו בביזה בעי, נתגלה בדרך זו (תחילה עלה בגורל שבטו, אחר כך מטהו, אחר כך משפחתו ולבסוף הוא עצמו). גם ביוון וברומא הטילו גורל, כדי ללמוד את רצון האל. אולם המושגים התיאורטיים המאפשרים מתן ביטוי לחוקיות המתגלה בהטלת גורל, בזריקת קוביות ובתהליכים מקריים דומים, לא התפתחו עד ימי פסקל, לייבניץ, הויגנס וברנולי.
אנשים שיחקו והימרו כבר בימי קדם, אך המושגים סיכוי והסתברות לא היו מוכרים בתרבות המערב עד המאה ה־17
בעולם העתיק, בימי־הביניים ובזמן החדש, נהגו מלכים ומושלים, מדינות, ערים ומקדשים, לממן את הוצאותיהם על־ידי מכירת קיצבאות. האזרח יכול היה לשלם סכום חד־פעמי ולקבל תמורתו קיצבה שנתית לכל ימי חייו, או כל עוד אחד מבני הזוג בחיים. היחס בין הסכום החד־פעמי שצריך היה להשקיע ובין גודל הקיצבה השנתית נקרא ״המכפיל״. לדוגמה: אם מישהו רוכש קיצבה של 1,000 שקלים לשנה תמורת השקעה חד־פעמית של 10,000 שקלים, הרי המכפיל במקרה שלו הוא 10. המכפיל תלוי בגיל רוכש הקיצבה (רוכש צעיר יותר צפוי ליהנות ממנה שנים רבות יותר. לכן הגיוני לדרוש ממנו מכפיל גבוה יותר), ובשער הריבית במשק (שער ריבית גבוה פירושו אשראי יקר, הגורם לכך שלמדינה כדאי למכור קיצבאות תמורת מכפיל לא־גבוה, אפילו לאנשים צעירים, כדי להשיג אשראי). כיום ברור לנו, שהמכפיל צריך להיקבע על סמך נתונים סטטיסטיים של תוחלת החיים השיורית בגילאים השונים.
בעולם העתיק לא היתה סטטיסטיקה כזאת. אף־על־פי־כן הכין אולפיָאנוס, משפטן רומי מן המאה השלישית, טבלת־מכפילים לרוכשי קיצבאות. בטבלה שלו, שהיתה כנראה מקובלת כבסיס לחישובים בקיסרות הרומית, המכפיל לרוכש קיצבה בגיל 20 שנה הוא 30, ובגיל 70 – 7. קביעות אלה חסרות כל בסיס תצפיתי או תיאורטי עקבי. הן הערכות על פי חוש ותו לו. בימי־הביניים נשתכחה אפילו הטבלה של אולפיאנוס, והחישובים התבססו על מכפיל קבוע, המתאים לתוחלת־חיים שיורית של 7 שנים בערך. כנראה שלצעירים לא היה אז כסף לרכוש קיצבאות או שלא היה להם עניין בהן.
יש מן האירוניה בעובדה, שדווקא במאה ה־19, כשהובהר הבסיס התיאורטי לחישוב המכפיל וכשהיו כבר נתונים לאומדן תוחלת־חיים שיורית, הפסידה המדינה כסף רב ממכירת קיצבאות. הדבר היה באנגליה ב־1808. הממשלה, שהיתה במצוקה כספית קשה, החליטה לממן את הוצאותיה על ידי מכירת קיצבאות בהיקף רחב, תוך שימוש במכפילים שייקבעו על־פי מיטב הידע המדעי ועל־פי הנתונים הסטטיסטיים החדשים. כבסיס לחישוב שימשו טבלאות־תמותה מן העיר נורתהמפטון, שערך ב־1780 ריצ׳ארד פרייס, פילוסוף ומתמטיקאי. פריים השתמש ברישומי הכנסיות של העיר נורתהמפטון להכנת עקומות המבטאות את אחוז הנפטרים בגילאים השונים, ועל־פיהן העריך את תוחלת־החיים השיורית לכל גיל. הוא הכין עבודה זו בשביל חברות־ביטוח, וכדי שלא לסכן אותן, הטה את אומדניו כלפי מטה. חברות ביטוח מפסידות בתוכניות ביטוח־חיים כאשר המבוטחים נפטרים לפני הגיל הצפוי, משום שאינם מספיקים לשלם את מלוא הפרמיה. הן נוטות על כן לאמץ אומדנים נמוכים של תוחלת־החיים השיורית מטעמי זהירות. במכירת קיצבאות, לעומת זאת, הסיכון למוכר (למדינה, לעיר) הוא בכיוון ההפוך. משמע, שהקיצבאי יחיה יותר מהצפוי ויזכה לקיצבאות רבות מהמתוכנן. כשהציעה ממשלת בריטניה לציבור את תכנית הקיצבאות החדשה, ביססה, כאמור, את חישוביה על הטבלאות של פרייס, שהיו מוטות לטובת חברות־הביטוח, ועל כן לרעת מוכרי הקיצבאות. תוך שנים מעטות נגרם לאוצר הבריטי הפסד של מיליוני לי״ש. היה צורך בחקיקה מיוחדת כדי לבטל את התכנית.

שני סוגי מדע
מושג ההסתברות ודרכי השימוש בנתונים סטטיסטיים הובהרו והתגבשו למן המאה ה־17 כפועל יוצא של שלושה תהליכים שהשתלבו זה בזה:
• תיאוריה מתמטית לחישוב סיכויים של מאורעות מקריים, שפיתחו פסקל, לייבניץ, הויגנס, ברנולי ואחרים
• היכולת לאסוף ולרשום נתונים בקנה־מידה גדול, עקב התפתחות המדינה המודרנית על מוסדותיה
• הפיכת החברה האנושית עצמה לנושא לימוד ומחקר פילוסופי, חברתי וכלכלי.34
ב־1836 הקים התוכן והמתמטיקאי הבלגי קטלה, המורה הרוחני של פלורנס נייטינגל, לשכה מרכזית לסטטיסטיקה בבלגיה, והיא הועתקה אחר־כך לכל המדינות המתקדמות. קטלה עקף את בעיית חירותו וייחודו של הפרט על־ידי מושג ״האדם הממוצע״, שטבע בספרו פיסיקה חברתית. מאורעות מקריים מתאפיינים בכך, שכל אחד מהם בפני עצמו אינו ניתן לחיזוי, אך הקבוצה, האוסף או הסידרה הנשנית של מאורעות כאלה הם בעלי תכונות יציבות שאפשר לאפיינן ולחזותן.
כשזורקים מטבע באקראי, אי־אפשר לדעת על איזה צד ייפול. ב־10 זריקות יש סבירות גבוהה למדי שהתוצאה ״עץ״ תתקבל בין 4 ל־6 פעמים. ב־100 זריקות יש סבירות גבוהה הרבה יותר, שהתוצאה ‘׳עץ״ תתקבל בין 40 ל־60 פעם, ובסידרה של 1, 000 זריקות יש כמעט ודאות, שהתוצאה ״עץ״ תתקבל בין 450 ל־550 פעם. משמע, בסידרה נשנית של זריקות מטבע, הולכת שכיחות התוצאה ״עץ״ ומתייצבת סביב מחצית מספר הזריקות.
התייצבות השכיחות היחסית של מופעי אירועים בקבוצות גדולות, היא הבסיס לביטוח. אדם שיש לו ספינת־סוחר אחת, שבה השקיע את כל רכושו, צפוי לחורבן כלכלי אם הספינה תטבע. כדי להתגונן מפני סכנה זו באמצעיו העצמיים, עליו להכין קרן שגודלה כמחיר ספינה נוספת, אפילו אם הנתונים מלמדים, שבספינות מן הסוג שבבעלותו שיעור הטביעה הוא 1 ל־100 לשנה. אבל, אם יתאגדו יחד 100 בעלי ספינות, יוכלו להניח בסבירות גבוהה, שמספר הספינות שיטבעו מקרב הצי שלהם לא יעלה על שתיים לשנה, ובממוצע לטווח ארוך יהיה השיעור ספינה אחת לשנה. אם כל אחד מהם ישלם פרמיית־ביטוח שנתית של שני אחוזים ממחיר הספינה, יקימו 100 בעלים שיתאגדו קרן שנתית בערך של שתי ספינות. הם יוכלו לפצות את מי שייפגעו באסון וגם לצבור רווח. אם תקום, לעומת זאת, חברת־ביטוח גדולה, כדוגמת ״לוידס״, ותבטח 10, 000 בעלי ספינות בכל רחבי־העולם, היא תוכל להוריד את פרמיית הביטוח השנתית ל־1.1 אחוזים ממחיר הספינה (כלומר, להקים קרן שנתית בערך של 100 ספינות הצפויות לטבוע), ולהיות עדיין רווחית. ככל שאוכלוסיית המבוטחים גדלה, כך אפשר להוריד את הפרמיה הנדרשת ולקרב אותה לערך הנזק הממוצע למבוטח, משום שהשכיחות היחסית של המאורע שמפניו מבטחים – טביעת הספינה הולכת ומתייצבת סביב ערכה הממוצע.
תורת ההסתברות המתמטית מאפשרת להעריך את הקשר בין גודל האוכלוסייה ובין הסטיות הסבירות של השכיחות היחסית מן הערך היציב שלה. סטיות אלה הן הסיכון האמיתי שנוטלות על עצמן חברות־הביטוח, ועל כן מאפשרת תורת ההסתברות לחשב את הפרמיה כך, שיובטח לחברת־הביטוח רווח הוגן ושמידת הסתכנותה לא תעלה על רמה נסבלת. חברות הביטוח נוהגות אף הן לבטח את עצמן כנגד אירועים חריגים אצל איגודי־ביטוח בין־לאומיים גדולים, כדי להגדיל עוד יותר את האוכלוסייה שבמסגרתה צריכה להתייצב השכיחות היחסית.
שכיחות המאורעות החריגים
התייצבות השכיחות היחסית של התוצאה ״עץ״ בהטלת מטבע סביב מחצית מספר הזריקות נראית כתופעת טבע, כמו נטייתו של ברזל להימשך אל מגנט, או כנטייתה של אבן להידרדר כלפי מטה. בכל זאת, יש הבדל בין שני סוגי התופעות. נטייתה של אבן להידרדר היא תכונה כללית של כל האבנים על פני כדור־הארץ, על הירח ובכל מקום שבו פועל כוח־המשיכה. אם ניתקל באבן, אשר במקום להידרדר תתחיל להתעופף כלפי מעלה, לא תנוח דעתנו עד אשר נמצא סיבה מיוחדת להתנהגות חריגה זו: התפוצצות זעירה מתחת לאבן שגרמה למעופה, סערה חזקה שטילטלה אותה באוויר וכיוצא באלה. לא כן הדבר בזריקת מטבע. אם ב־1,000 זריקות תתקבל התוצאה ״עץ״ רק 300 פעם, נהיה מופתעים, נבחן את מנגנון הזריקה ואת האפשרות שהמטבע אינו סימטרי. אבל אם יסתבר שהכול כשורה, נוכל להתנחם בטענה, שהתוצאה החריגה שקיבלנו, אינה בלתי־אפשרית לחלוטין, וכי אם היא מתרחשת אחת לאלפיים סדרות ניסויים, אין בכך משום חריגה.
אין לדעת מי ירצח בישראל בשנה הבאה, אך אפשר להעריך אח מספר מקרי הרצח שיתרחשו
ומה בדבר פלורנס נייטינגל? האם אין אפשרות שירידת אחוז התמותה החודשי בקרב הפצועים בבית־החולים הצבאי שבהנהלתה היתה תופעה מקרית, כמו קבלת התוצאה ״עץ״ 300 פעם ב־1, 000 זריקות? ואם קיימת אפשרות כזאת, מה הבסיס לטענה, שירידת התמותה היא פרי מאמציה של האחות?
האפשרות אכן קיימת, אבל סבירותה נמוכה מאוד. ירידה מקרית של התמותה מ־42 אחוזים ל־2. 2 אחוזים היא אירוע כה נדיר, שאפשר וכדאי להסתכן בהימור נגדי ולטעון, שהדבר לא היה פרי המקרה, אלא תוצאת השיפורים שהוכנסו בשיטות הסיעוד. דומה שהגענו להבחנה שהיתה רווחת במאה ה־19 ובראשית המאה ה־20 בין ״המדעים המדויקים״ – מתמטיקה, פיסיקה, אסטרונומיה, לבין מדעי האדם -רפואה, כלכלה, סוציולוגיה. המדעים המדויקים, כך סברו אז, הם דטרמיניסטיים. חוקיהם בעלי תחולה כללית, ללא חריגה, ללא יוצא מהכלל. טענותיהם ניתנות להוכחה או להפרכה, הן אמיתיות או שקריות. מדעי האדם, לעומת זאת, הם בעלי אופי הסתברותי. חוקיהם מתארים את המתרחש ב״רוב המכריע״ של המקרים, אך יש בהם פתח לחריגה, לאירוע בלתי־ טיפוסי. הטענות במדעים אלה הן בעלות סבירות גבוהה או נמוכה, ולא בהכרח אמיתיות או שקריות. ככל שהאוכלוסיות שמדעי־האדם עוסקים בהן (אוכלוסיית בני־אדם, אוכלוסיית תצפיות, אוכלוסיית ניסויים) גדולות יותר, כך הם הולכים וקרבים באופי חוקיהם וטיעוניהם למדעים המדויקים, אך אינם מגיעים אף פעם לוודאות גמורה.
משנות ה־20 של המאה הנוכחית התחילו להופיע סימני־שאלה הן לגבי מהותה ומשמעותה של תופעת השכיחות היחסית ההולכת ומתייצבת והן לגבי ההבדל בין שני סוגי מדע אלה.
הסתברות אובייקטיבית וסובייקטיבית
אדם מגיע הביתה בערבו של יום ומוצא שהדלת אינה נעולה. כשהוא נכנס הוא מגלה חפצים מוטלים על הרצפה, ארונות פתוחים וקופסאות שתוכנן הוצא ופוזר. מה קרה? הוא שכח לנעול את הדלת בצאתו והשאיר מהפכה בבית? הבת הגיעה לחפש משהו ומיהרה לצאת? גנב? האפשרות השלישית נראית סבירה משתי האחרות, גם בגלל35 האי־סדר וגם משום שכמה דברי־ערך חסרים. הוא מחליט לטלפן למשטרה.
״יש לי סיכוי טוב להתקבל לעבודה״, ״יש לי סיכוי טוב לקבל שני קלפים מאותו צבע״ - מה ההבדל?
בסיפור זה, כמו בדיון על הביטוח, על הקיצבאות ועל הרפואה בצבא, מובלע המושג ״הסתברות״. בפני גיבור הסיפור עמדו כמה הנחות חלופיות, ועל פי עדויות עקיפות יכול היה לייחס להן הסתברות יחסית. בסופו של דבר נקט פעולה המתחייבת מן ההנחה, שנראתה לו סבירה מכולן. כיצד אפשר לקשר את ההסתברות הגבוהה יותר שמייחס גיבור סיפורנו להנחה ״היה גנב״ לעומת ההנחה ״שכחתי לנעול את הדלת״, למודל של שכיחויות יחסיות יציבותי אפשר לומר: ההסתברות הגבוהה יותר של ההנחה ״היה גנב״ משמעה, שבמספר רב של מקרים שבהם חזרו אנשים הביתה ומצאו מהפכה, התברר, שאכן היה גנב ורק במיעוטם נמצא הסבר אחר. האם נתונים אלה היו ידועים לגיבור, והאם הביא אותם בחשבון כשהחליט לטלפן למשטרה? קרוב לוודאי שלא. יש, ככל הנראה, מובן נוסף למושג ההסתברות, שאפשר לתאר אותו כדרגת־ההאמנה, הנסמכת על עדויות ועל נתונים שונים, שאינם בגדר אימות גמור או הפרכה גמורה. הייתכן שמשמעות זו של מושג ההסתברות – דרגת־ההאמנה – אינה קשורה למשמעות הקודמת של שכיחות יחסית יציבה, וכי הצד השווה הוא רק השימוש הלשוני באותו מושג בשני הקשרים שונים? יש סבורים כך, ונמצאו אף מי שהציעו להפריד בין שני המובנים על ידי מונחים נבדלים. ההצעה לא צברה תמיכה, אולם החל בירור מעמיק של מושג ההסתברות ושל משמעויותיו.
אסכולה אחת, שנציגה הבולט הוא המתמטיקאי והפילוסוף הגרמני ריכרד פון מיזס, דבקה בעקביות בשכיחות היחסית כבמשמעות הלגיטימית היחידה של המושג הסתברות. היא ביקשה לפרש כל שימוש במושג זה על דרך השכיחות. לדעת אנשי אסכולה זו, אין זה חשוב אם גיבור הסיפור ידע את נתוני השכיחות כשהחליט לטלפן למשטרה. הדיון שעשה בינו לבין עצמו בהנחות השונות, התאפשר מכוח העובדה, שבמקרים רבים אחרים למד לקשר בין ממצאים ראשוניים כגון ״חסר כסף״ ובין ראיות חותכות למציאות גנב.

אולם מה פירושה המדויק של הפרשנות על דרך השכיחות? כשאנו אומרים שההסתברות לקבלת ״עץ״ בהטלת מטבע היא 1/2, כיצד בדיוק יש לפרש זאת על דרך השכיחות? אמרנו, שבסדרה ארוכה של הטלות מטבע מקריות, הולכת השכיחות היחסית של התוצאה ״עץ״ ומתייצבת סביב מחצית מספר ההטלות. בהסבר זה יש שני קשיים: האחד, מה פירוש ״סדרה36 מקרית״ של הטלות וכיצד מבחינים בין סדרה מקרית לסדרה בלתי־מקרית בלי להפוך את ההגדרה למעגלית, והשני, מהי ״סדרה ארוכה״, מה צריך להיות אורכה והאם לא נכון שגם בסדרות ארוכות מאוד תיתכן שכיחות יחסית הסוטה מ־1/2, אף־על־פי שאפשרות זו היא בעלת סבירות נמוכה.
תורתו של פון מיזס מגדירה את המושג ״סדרה מקרית״ בצורה לא־מעגלית ועוסקת בשכיחות יחסית של סדרות ניסויים אין־סופיות. בעשותה כך, היא מתגברת על הקשיים שהזכרנו, אבל מאבדת חלק מן המובן האינטואיטיבי של המושגים ״סדרת ניסויים מקרית״ ו״שכיחות יחסית״. עובדה זו שימשה גורם מדרבן למתן פשר למושג ההסתברות מכיוון שונה.
דה־פִינֶטי, ראמזֵי וסֶבֶג׳ יצאו דווקא מתוך המובן הסובייקטיבי של המושג הסתברות כדרגת האמנה, וביססו עליו גם את משמעות השכיחות היחסית. לדידם, מושג ההסתברות בכל הֶקשר מהקשריו משקף את מצב הידע (הלא־שלם) שלנו על העולם. התצפיות גורמות לנו לעדכן אותו, אך הוא נשאר תמיד בחזקת ידע סובייקטיבי. ״ההסתברות לקבלת ׳עץ’ בזריקה מקרית של מטבע היא 1/2״ – אינו, לדידם, היגד אובייקטיבי על המטבע, אלא היגד סובייקטיבי, המשקף לעתים קרובות בעיקר אי־ידיעה, חוסר יכולת לבסס את התוצאה ״עץ״ דווקא או את התוצאה ההפוכה.
שני הסברים אלה של מושג ההסתברות הם קיצוניים. אין הכרח לצדד באחד מהם באופן בלעדי. יש כנראה נושאים, שבהם אנו נוטים לייחס להסתברות משמעות אובייקטיבית, כגון בהטלת מטבע, בתוחלת־חיים שיורית ובנתוני התמותה של בתי־החולים. בתחומים אחרים, כמו עדויות משפטיות, אמינות של מוצרים שטרם נוסו, בטיחות או הערכות מחיר של מוצרים בפיתוח, ההסתברות נראית סובייקטיבית בעיקרה.
מהי ההסתברות לכך, שלשמשות בשביל־החלב יתלוו כוכבי־לכת? לשאלה זו יש תשובה אובייקטיבית. יצור עליון בעל ידע מקיף ומפורט על היקום יכול לחשב את השכיחות היחסית של שמשות בעלות כוכבי לכת בשביל־החלב שלנו ובגלאקסיות אחרות, ולהעריך בדרך זאת את שכיחות התופעה. לנו, על פני כדור־הארץ, אין אפשרות לאמוד את ההסתברות האובייקטיבית הזאת על־ידי דגימות וסקרים, כי אמצעי התצפית שלרשותנו אין בכוחם לגלות כוכבי־לכת של שמשות אחרות אפילו בשביל־החלב שלנו, אלא לכל היותר
בסביבתנו הקרובה. אף־על־פי־כן אין זה מונע אותנו מלשער השערות המבטאות ידע בתהליכי היווצרות כוכבי־לכת, השערות לגבי יציבותם ותלות היציבות בגודל השמש וכדומה. על־פי נתונים אלה אנו בונים את ההסתברות הסובייקטיבית שלנו. לא תמיד יש לה ערך מספרי מדויק. לעתים היא מגדירה רק תחומים, כגון, ״שמשות בעלות כוכבי־לכת מהוות חלק קטן מאוכלוסיית השמשות בשביל החלב״. עם שיפור אמצעי התצפית והרחבת הידע המדעי משתנה ההסתברות הסובייקטיבית שלנו ומתקרבת באופן הדרגתי, כפי שאנו מקווים, אל ההסתברות האובייקטיבית, שבשלב זה איננה בת־השגה.
ההימור של פסקל
גם הסתברות סובייקטיבית כפופה לתחשיב בעל כללים מוגדרים כשהיא אמורה לשמש בסיס לפעולה, כלומר, לקבלת החלטה בתנאי אי־ודאות, לברירה בין חלופות על־פי שיקולים רציונליים. אותו תחשיב חל גם על ההסתברות האובייקטיבית, וזוהי אחת הסיבות לכך, שנוטים לראות בהן שתי פנים של אותו מטבע. פסקל, הפילוסוף והמתמטיקאי הצרפתי בן המאה ה־17, היה ממעצביה וממניחי יסודותיה של תורת ההסתברות. הוא השתמש בה לפתרון בעיות בתחום ההימורים, כגון, כיצד יש לחלק את הקופה בין המשתתפים השונים במשחק הימורים שנפסק באמצע. הוא השתמש בה גם למטרה אחרת – הוכחת מציאות האל.
בקטע ״אין סוף – לא כלום״, בספר הגיגים, עוקף פסקל את השאלה המטאפיסית של קיום האל ומתרכז בבעיית החלטה קונקרטית: האם לחיות על־פי ההלכה הדתית ולהתנהג כאילו היה האל קיים, או שמא מוטב להתעלם מכך ולחיות חיי־שעה. פסקל ניגש לבעיה זו על־פי עקרונות שחידש ושנעשו אחר־כך בסיס לתורת ההחלטות המודרנית. הגמולים הצפויים בכל אחת משתי דרכי־הפעולה האפשריות הם: גאולת הנפש, אם האל קיים ואם נחיה על־פי המצוות, ואבדון אם האל קיים ואנו נחיה את חיי העולם הזה. אשר לגמולים במקרה שהאל אינו קיים מניח פסקל, בשלב הראשון, כי אין הבדל רב ביניהם.
לאחר שהבעיה הוצגה בצורה זו עלינו להחליט או, כלשון פסקל, עלינו להמר על אחת מדרכי־הפעולה הפתוחות בפנינו. אם מצב־העולם הוא ״האל אינו קיים״ – אין הבדל משמעותי בין ההימורים. אך אם המצב הוא ״האל קיים״, הרי החיים על־פי מצוות הדת,
המביאים גאולה, עדיפים לאין ערוך על חיי העולם הזה, המביאים אבדון. לכן ההימור על חיי מצווה עדיף, ויש לנקוט אותו ולהגיע בדרך זו אל האמונה.
אולם, אומר פסקל, אפשר לחלוק על הטענה הקודמת ולומר, שבמצב ״האל אינו קיים״ אין הגמולים של שתי דרכי־הפעולה שקולים. פסקל אינו מפרט בנקודה זו, אך אפשר להניח, שכוונתו לומר, כי מי שיחיה חיי מצווה, ימנע מעצמו הנאות ולא יוכל להשיג הישגים, משום שלא כל האמצעים יהיו כשרים לגביו. מבחינות אלה יהיה יתרון למי שיבחר בחיי העולם הזה, אשר בפניו לא יהיה כל מעצור.
האם לחיות על פי ההלכה הדתית ולהתנהג כאילו האל קיים, או שמוטב לחיות חיי שעה
בהנחה חדשה זו אין עוד עדיפות גמורה לאחת מדרכי־הפעולה. לכל אחת יש יתרון באחד ממצבי־העולם. זהו מצב אופייני בבעיות החלטה: יש פנים לכאן ולכאן. כיצד נבחרי פסקל נותן תשובה שעד היום לא נמצאה טובה ממנה: על־פי תוחלת הגמול. יש להעריך את ההסתברות של כל אחד ממצבי העולם, ולחשב את הגמול המשוקלל של כל דרך־פעולה באמצעות הסתברויות אלה. אחר־כך יש לבחור באותה דרך־פעולה שבה התוצאה המשוקללת, שהיא תוחלת הגמול, מקסימלית.
פסקל יודע, שכדי לחשב את תוחלת הגמול צריכה להיות אמת־מידה כמותית אחידה, שתאפשר את השוואת האבדון לגאולה, להנאות העולם הזה ולחיים של שלילת הנאה. הוא בוחר כאמת־מידה את הנאות העולם הזה, או ביתר דיוק את הפער שבין הנאה לבין שלילתה. זוהי ״יחידת גמול״ אחת. נתבונן עכשיו בפער שבין גאולה לאבדון: מה גודלו לעומת הנאות העולם הזה?
ברור לפסקל, שמבחינה איכותית יש לגאולה יתרון מוחלט על פני הנאות העולם הזה, אך הוא מוכן להתעלם מן ההבדל האיכותי ולהתרכז בהיבט הכמותי בלבד. אילו היתה הגאולה מובטחת למשך מחזור חיים אחד (לאחר המוות), היא היתה שקולה מבחינה כמותית להנאות העולם הזה. אילו היתה מובטחת למשך שני מחזורי חיים, היה משקלה עולה כפליים על זה של חיי העולם הזה, שמשכם הוא מחזור־חיים אחד. אבל הואיל והגאולה היא לנצח, הרי מבחינה כמותית משקלה גדול לאין־סוף ביחס להנאות העולם הזה.
נניח שאגנוסטיקן, היינו, אדם שאינו יודע לקבוע אם האל קיים או אינו קיים, מייחם לשתי האפשרויות משקל שווה, כלומר, נותן למצב העולם ״האל קיים״ הסתברות סובייקטיבית של 50 אחוז ולמצב ״האל אינו קיים״ – אותה37 הסתברות עצמה. אם אדם זה יעריך את הגאולה כשוות־ערך להנאות העולם הזה, ימצא ששתי דרכי־הפעולה – חיי מצווה וחיי העולם הזה – שקולות זו כנגד זו מבחינת תוחלת הגמול. אם, לעומת זאת, יקנה איש זה לגאולה ערך כפול, משולש או אף גבוה יותר, ביחס להנאות העולם הזה, יצטרך להעדיף חיי מצווה מבחינת תוחלת הגמול.
מולך בא קירחַ המרכיב משקפיים: האם הוא ספרן או חקלאי?
נתייחס עכשיו לאגנוסטיקן מטיפוס אחר, שבעיניו ״האל אינו קיים״ היא אפשרות סבירה הרבה יותר מהאפשרות ״האל קיים״, נאמר, ביחס של 99 ל־1. כלומר, הוא מייחס למצב ״האל אינו קיים״ הסתברות סובייקטיבית של 99 אחוזים ולמצב ״האל קיים״ הסתברות סובייקטיבית של 1 אחוז בלבד. בכמה צריך הוא להעריך את הגאולה ביחס להנאות העולם הזה, כדי להגיע לתיקו? התשובה ברורה – פי 99. אבל אם הגאולה עולה בערכה הכמותי על הנאות העולם הזה בשיעור גדול יותר, יצטרך גם הוא להעדיף את האפשרות של חיי מצווה, אף־על־פי שהוא מייחם סבירות כה נמוכה לקיום האל.
הואיל והגאולה אין־סופית בערכה הכמותי ביחס לחיי העולם הזה, נגיע בהכרח למסקנה, שכל מי שאינו בחזקת כופר גמור, כלומר, כל מי שמוכן לייחס הסתברות חיובית, קטנה ככל שתהיה, למציאות האל, יגיע בעל כורחו למסקנה, שעליו לבחור בחיי מצווה ולהגיע בדרך זו לאמונה באל.
אפשר לתאר את המצב באמצעות טבלה:
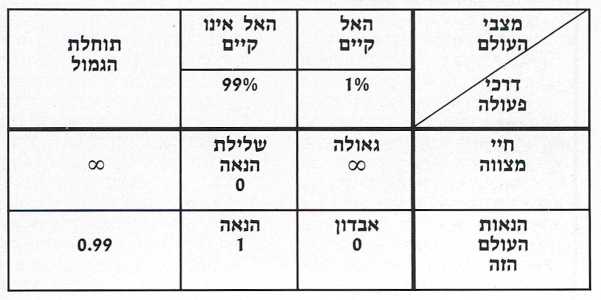
ההימור של פסקל כבעיית החלטה
ההימור של פסקל עורר פולמוס חריף ב־300 השנים האחרונות. נכתבה ספרות ענפה השוקלת, מנתחת ומבקרת אותו על כל פרטיו ודקדוקיו. כיום מקובלת הדעה, שכמה וכמה הנחות שמניח פסקל אינן עומדות בפני הביקורת ולכן ״הוכחתו״ למציאות האל אינה תקפה. אולם שיטת הדיון ועקרונות תורת ההחלטה, שבהם משתמש פסקל, תקפים ועומדים בעינם עד היום. מכל מקום, ההימור של פסקל מבליט את משמעותה של ההסתברות הסובייקטיבית: המשקל היחסי שמקנה המחליט למצבי העולם השונים – משקל שעל־פיו הוא מחשב את תוחלת הגמול בכל אחת מדרכי הפעולה האפשריות ובוחר בדרך הפעולה המועדפת – משקל זה משקף את עמדותיו הסובייקטיביות ולא תמיד אפשר לבססו באופן אובייקטיבי.
חידת הקרחת והמשקפיים
בחמישים השנים האחרונות חל מפנה מעמיק במעמדן התיאורטי והתרבותי של ההסתברות ושל הסטטיסטיקה. ביטויים כמו ״אני בטוח ב־90 אחוז״, ״יש סיכוי נמוך שצירוף כזה היה מקרי״, ״ההסתברות לזכות בפיס היא כמו ההסתברות להיפגע בתאונה״ חדרו ללשון הדיבור. אמצעי התקשורת מפרסמים נתונים סטטיסטיים על גודל האוכלוסייה, על הפעילות בבורסה ועל הסיכון לסרטן־ריאות אצל מעשנים. סקרי דעת־הקהל פועלים באמצעות מדגמים, ודגימות מאפשרות חיזוי מדויק למדי של תוצאות בחירות, שעות רבות לפני שספירת הקולות הושלמה. אולם, במקביל החלו גם להופיע כשלי היגיון, הוכחות מדומות וטיעוני־סרק, שמקורם במערכת המושגים החדשה.
אתה הולך ברחובה של תל־אביב. מולך בא מישהו בלתי־מוכר, קירח ומרכיב משקפיים. על אלו משתי האפשרויות תהמר: שאדם זה הוא ספרן או שהוא חקלאי? אחרי הרהור קל אתה מגיע למסקנה שקרחת ומשקפיים אופייניים לספרנים יותר מאשר לחקלאים, ומחליט להמר על כך שהאיש הוא ספרן.
נכשלת. נניח שאתה צודק ושקרחת ומשקפיים שכיחים בקרב ספרנים פי 10 מאשר בקרב חקלאים. אך מהו היחס המספרי בין ספרנים לחקלאים ברחובותיה של תל־אביב? אוכלוסיית הספרנים בארץ כה קטנה, שנוכל להניח כי מספר החקלאים המהלכים ברחובות גדול ממספר הספרנים לפחות פי 100. בתנאים אלה יש עדיין סיכוי של 10 ל־1, שהאדם שפגשת הוא חקלאי ולא ספרן, למרות המשקפיים והקרחת.
במקרה זה נובע הכשל מניתוח לא־שלם של הנתונים, הצריכים לשמש בסיס להימור. במקרים אחרים, מבחר הנתונים עצמו הוא מקור הבעיה.
לעתים הטעות נובעת מכך, שהמקרים הממקדים את תשומת־לבנו אינם כל המקרים, אלא הבולטים שבהם. עובדה זו יוצרת הטיה המוליכה למסקנות המוטעות. פרסומם של38 מרפאים, ידעונים ומלחשים למיניהם נשען על תהליך כזה. המקרים שבהם הידעוני ״יודע״ היכן החפץ האבוד, המלחש מצליח ״להסיר״ בלחשו כאב־ראש מטריד, והמרפא מעלה ארוכה, כביכול, למחלה חשוכת־מרפא, בולטים מאוד. הנוגעים בדבר מתרגשים ושמחים ומפרסמים את ה״נס״ ברבים, ואילו בכל המקרים האחרים שבהם הפונים נכשלים, הם מתביישים, בדיעבד, בחולשתם ומסתירים את עצם הפנייה לידעונית. רק לעתים רחוקות נמצא מי שמדבר על כך, וגם אז אין סיפור הכישלון בגדר ״חדשות״. יוצא, שהמידע המגיע לידיעת הציבור עוסק רובו בהצלחות והוא תורם ליצירת הסתברות סובייקטיבית בלתי־מבוססת, לאמור: לנוקטים שיטות בלתי־מקובלות יש הצלחה ניכרת.
הטיה זו קיימת לא רק בציבור הרחב, אלא גם אצל המרפאים והידעונים עצמם. שהרי מי שבעייתו לא נפתרה, או אף הוחמרה, מתנתק מהם עד מהרה, ואילו מי שחל אצלם שיפור מתחזקים באמונתם וממשיכים בקשר, גם אם אין כל ראיה לכך שהשיפור מקורו בטיפול. כך נוצרת הטיה המביאה לתשומת-לבו של המטפל עצמו מספר גדול יחסית של הצלחות. הוא משתכנע על־כן באמת ובתמים בכוחן של שיטותיו.

פראדוקס העורבים
יש במושג ההסתברות קשיים עמוקים יותר, והדרך להתגבר עליהם או לעוקפם עודנה שנויה במחלוקת. הפילוסוף והלוגיקן בן דורנו, ג׳ורג המפל, הציג בעיה: חוקר ציפורים משער שכל העורבים שחורים. בכל פעם שהוא מגלה עורב שחור, גוברת ההסתברות שהשערתו נכונה. אולם הפסוק ״כל עורב הוא שחור״ שקול לחלוטין מבחינה הגיונית ל״כל מה שאינו שחור – אינו עורב״. אותו חוקר מוצא בביתו כיסא לבן, והדבר מגדיל, לכאורה, את ההסתברות לכך שהשערתו בעניין העורבים נכונה. הפראדוקס של המפל מכונה לעתים ״צפרות בית״, כי הוא מאפשר לכאורה לצפרים לאסוף נתונים על העופות מבלי לצאת מהסלון.
פראדוקס העורבים מלמד על בעיית־יסוד בתהליך האינדוקטיבי, שהוא תהליך בסיסי במדע: הגדלת סבירותן של השערות על ידי צבירת נתונים המאשרים אותן. שימוש פשטני ולא־ביקורתי בתהליך זה מוליך לקשיים ולסתירות, שפראדוקס העורבים הוא רק אחד מהם.
בשנות ה־20 קבעה ג׳יין ניקוֹד את הכלל הקרוי על שמה: כל תצפית המאשרת שעצם מסוג א׳ הוא בעל תכונה ב׳, מגדילה את סבירות החוק הכללי – ״כל העצמים מסוג א׳ הם בעלי תכונה ב׳״ (ברור שכל תצפית נגדית של עצם מסוג א׳, שאינו בעל תכונה ב’, מפריכה את החוק אחת ולתמיד). הפראדוקס של המפל מלמד, שאי־אפשר לקבל את כלל ניקוד בצורה פשטנית.
כדי להבין זאת נתבונן בדוגמה: בסביבתנו מיליון עצמים ובתוכם אלף עורבים. אשר לעצמים שאינם עורבים כ־10 אחוזים מתוכם שחורים והשאר לא־שחורים. אנו בוחנים שני סוגי ניסויים במטרה לקבוע את צבעם של העורבים בסביבתנו:
• לוכדים באקראי עורב ובוחנים את צבעו.
• בוחרים באקראי עצם לא־שחור ובוחנים את עורביותו.
האם הכיסא הלבן מעיד על כך שכל העורבים שחורים?
נניח שכל העורבים שחורים. במקרה זה נקבל בשני סוגי הניסויים תוצאה ברורה: כל עורב שנלכוד יהיה שחור וכל עצם לא־שחור, שנבחר באקראי, יהיה לא־עורב. עתה נבחן הנחה אחרת, שבין אלף העורבים יש 200 לבנים והשאר שחורים. ההסתברות שלכידת עורב באקראי תפריך את החוק שכל העורבים שחורים, היא 20 אחוז. לעומת זאת, עצם לא־שחור, אקראי, יהיה עורב, רק בכשתי מאיות האחוז מן המקרים. אפילו אם נניח הנחה קיצונית יותר – שכל העורבים בסביבתנו לבנים, הרי הסיכוי שנפריך את הטענה המוטעית, שכל העורבים הם שחורים, על־ידי ניסוי מן הטיפוס השני, הוא רק 1/900 כלומר, כ־1/10 האחוז.
עלינו לקבוע אפוא, בניגוד לכלל ניקוד, שתוצאה חיובית בניסוי יכולה להיחשב כאישור לחוק כללי, רק כאשר ההסתברות לקבלת תוצאה שלילית, בהנחה שהחוק אינו תקף, היא משמעותית. העובדה שמי ששתה תה בלימון החלים משפעת, אינה יכולה לשמש אישור לחוק כללי האומר, ששתיית תה בלימון מביאה להחלמה משפעת. היא תוכל להיחשב כאישור רק אם יתברר גם, שאי־שתיית תה בלימון מאריכה או מחמירה באופן משמעותי את מחלת השפעת.
מושג ההסתברות (הסובייקטיבית והאובייקטיבית) יש בו אפוא רבדים עמוקים יותר מאלה המתבטאים ביציבותן של שכיחויות, או בתחשיב לדרגות־האמנה. שאלה בסיסית היא, מה בכלל אנו מכנים בשם ״תופעה״, איזו תכונה ראוי שנייחס לה שכיחות והסתברות, ואיזו לא. כשאנו זורקים מטבע פעמים רבות, מדוע מתייחדת תשומת־לבנו דווקא לצד שעליו הוא נופל ולא לתופעות אחרות, כגון הצליל שמשמיע המטבע או מספר הפעמים שהוא מתנדנד אנה ואנה עד שהוא מגיע למנוחה – תופעות שבהן שכיחות התוצאות אינה מתייצבת. קוואין, מחשובי הלוגיקנים של תקופתנו, מדבר על ״תכונות טבעיות״. חוקים כלליים מתנסחים ונבחנים לגבי תכונות טבעיות. מבחינה זו הן עומדות ביסוד ההסתברות וביסוד המדע בכלל. לעומת זאת משתנות השקפותינו, ועמן תמונת העולם שלנו בכללה, עקב השינויים בתרבות ובמדע, והדבר משפיע גם על ״טבעיותן״ של תכונות. תופעות חדשות נראות טבעיות ואחרות, שנראו טבעיות, חדלות להיות כאלה. בדרך זו מתרחש משחק־גומלין עדין וסמוי בין המחשבה המדעית ובין התרבות בכללותה, והשתיים תלויות זו בזו ומפרות האחת את רעותה. ■39