הקדמה:
ליאונרדו דה וינצ׳י אמר שרק הציור יכול לתאר את שלל הצורות בטבע, ולכן מי שמקל ראש בציור סופו שיקל ראש גם במדע. שכן המדע, כמו הציור, משתמש בחשיבה פילוסופית כדי להבין את צורות החי והצומח. אני מניח שהשקפתה של פרופ׳ גילה בלס על הציור קרובה יותר לדה וינצ׳י מאשר להשקפתו של אפלטון, שראה בציור אמנות פחותה, כיוון שהיא מחקה את העצמים שהם עצמם מעשה חיקוי של הצורות האידיאליות. במרכז הרצאתה של גילה בלס עומד חתך הזהב, אשר היתה לו השפעה רבה על התפתחות הציור והארכיטקטורה, ואשר במשך תקופה ארוכה נחשב למבטא הנאמן ביותר של היופי האמיתי.

המספר המכונה ״מספר זהב״ הוא מספר לא רציונלי, שהנוסחה המתמטית שלו היא
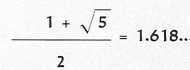
במאה ה-12 המציא המתמטיקאי ליאונרדו מפיזה (המכונה פיבונאצ׳י) טור מספרי שערכיו הראשוניים הם: …21, 13, 8, 5, 3, 2, 1. טור זה, הקרוי על שם ממציאו “טור פיבונאצ׳י״, מאפשר לחשב במספרים שלמים ערכים קרובים למספר הזהב. הוא ממחיש את תכונתו המיוחדת של המספר כמוצר של יחס, שבו הערך השלישי, שבלעדיו לא מתקיים קשר יחסי, הוא תמיד הסכום של שני הערכים הקודמים לו. המונח “חתך הזהב” (Golden Section) הוטבע על ידי לוקא פאצ׳ולי בספרו “הפרופורציה האלוהית”, שראה אור בוונציה בשנת 1509 בלוויית רישומים של ליאונרדו דה-וינצ׳י.
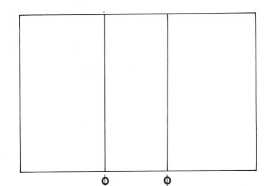
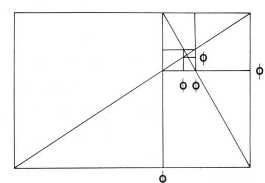
מונח זה מגדיר יחס גיאומטרי ומציין את הנקודה שבה מתחלק קו לשני חלקים לא שווים, באופן שהחלק הגדול (a) מתייחס אל החלק הקטן (b) כמו השלמות (a + b) אל החלק הגדול (לוח 1א). חלוקה כזאת אינה מחייבת חישובים מתמטייים מורכבים; אפשר לבצעה באופן פשוט ביותר באמצעות סרגל ומחוגה. כשמדובר בקו, אם כן, חתך הזהב הוא נקודה. במשטח הוא הקו שמחבר בין שתי נקודות חתך זהב זהות שעל הקווים של שתי צלעות נגדיות (לוח 1ב). ובכן, את חתך הזהב מייצגים קווים ונקודות, אך יש גם מלבן זהב, שבו הגובה מתייחס לרוחב ביחס של חתך זהב. התכונה המיוחדת של חתך הזהב היא שהוא מייצג פרופורציה (יחס) היכולה להתפתח מתוך עצמה עד אין סוף בשני כיוונים: אל הגדול מכל ואל הקטן מכל (לוח 2). מטילה גיקה (Matila Ghyka), בספרו “חתך הזהב” משנת 1931, הנהיג את הסימון של מספר הזהב וחתך הזהב באות היוונית פי (Ф), כרמז לאות הראשונה בשמו של פידיאס, גדול הפסלים היווניים בעת העתיקה. בדרך זו ביקש לסמל את38 הקשר בין הנוסחה המתמטית לבין האידיאה של היפה.


הפסל הישראלי יגאל תומרקין נוהג לשלב את הנוסחה המתמטית ברבות מעבודותיו. דוגמה אופיינית לכך היא הרישום “ג׳רבה״ (1979), שהוצג בתערוכתו במוזיאון תל אביב בשנת 1980 (תמונה 3). מצד ימין שיבץ האמן בהדגשה את הנוסחה המתמטית של מספר הזהב, ומשמאל, מתחת לנוסחה הכימית של המים (h2O), כתב על התרשמותו מג׳רבה בתוניס. ברישום נראים רועה, כבשים, ציפור, וכן, על קו האופק המוגבה, צילום של מבנה עתיק (קבר, או מצבה, מבנה פולחני). באמצעותם מציג האמן סוג של מקום וזמן שהוא מייחס להם חשיבות ושיש להם עבורו משמעות מיוחדת. המקום מוגדר כמרחב מזרחי ים תיכוני, והזמן כשייך בו זמנית למציאות פסטורלית עממית על זמנית ולתרבות העתיקה של האיזור. באמצעות הטקסט, לעומת זאת, מביע האמן התייחסות אסתטית וקיומית למקום, שהוא ״יפה״ (נוסחת מספר הזהב) ושהוא “הכרחי״ כמקור של מים, של חיים (נוסחת המים). במרכז הרישום משורטט מלבן שהוא פחות או יותר מלבן זהב. קו חתך הזהב שלו מימין חוצה את דמות הרועה ואת העיגול של ראשו באופן שהוא יכול להיקרא כאות פי (Ф), וכך גם העיגול של האות O, שדרכו עובר קו חתך הזהב משמאל. כך נוסף להיבט של המקום (האידילי והאידיאלי) ושל הזמן (ההיסטורי), ממד עכשווי, קונספטואלי.
דוגמה אחרת היא עבודה של האמן האיטלקי מריו מרץ Mario Merz)39) המכונה “טור פיבונאצ׳י על מדרגות” (1971, תמונה 4).

זהו צילום של חדר מדרגות, דל ולכאורה פשוט מאוד, נעדר קישוטים, שאינו מעביר שום מידע ערכי על המקום כשלעצמו. כצילום, לעומת זאת, הוא מתוכנן בקפידה, כששני קווי הגובה העיקריים שלו חופפים לחתכי זהב לא סימטריים של מלבן הפורמט. על המדרגות הציב האמן מספרים ברצף של טור פיבונאצ׳י עולה (תרתי משמע); בצד שמאל למעלה קבועים כמה מספרים, כשהאור הדלוק בהם והצינורות מובילי החשמל (הנראים בצילום כקווים) “מוחקים״ אותם ומדגישים את אינסופיות הטור. המסר בעבודה קונספטואלית זו טעון מאוד, וניתן לפרשו בדרכים אחדות. כאן היא מעניינת אותנו כדוגמה נוספת לשימוש המושגי שעושים אמנים בני זמננו בנוסחאות מתמטיות כסימנים של ה׳׳יפה״.
מספרים אלוהיים החבוים בטבע
נשאלת אפוא השאלה מה מייחד את היחס של חתך הזהב, כיצד הוא מתקשר עם המושג של ה׳׳יפה” ומדוע דווקא הוא הפך לסמל מייצג שלו באסתטיקה המערבית.
למספר הזהב בתור אינדיקטור של היפה יש שני היבטים: האחד פילוסופי-אסתטי שמקורו במחשבה היוונית בעת העתיקה, ואשר בעקבותיו נוצר במרוצת הזמן מעין מיתוס על מספרים וצורות מושלמים, “אלוהיים״, המוצגים כסמל של היופי המושלם בכל התקופות. השני, הנובע מהראשון והמותנה על ידו, הוא מתמטי-מעשי: שימוש הולם בנתונים המיוחדים של הפרופורציה של חתך הזהב עשוי לעזור לאמנים לבנות קומפוזיציה ״יפה״, וזאת, כאמור, הודות לכך שחתך הזהב מאפשר חלוקה א-סימטרית, אך מאוזנת ומתמשכת, של קו או של פני משטח נתונים. חלוקה כזאת מאפשרת לשמר מתח במסגרת כוללנית מאוזנת (הרמונית) ולהעניק ליצירה תחושה של תנועה וחיים. תכונות מיוחדות אלו של חתך הזהב היו מוכרות לאמנים ושירתו אותם מהעת העתיקה, ויש אומרים אפילו מתקופת מצרים העתיקה, ומוסיפות לשרתם עד היום.
הטקסט הבא מתוך “טימאוס” לאפלטון מעיד, כי היוונים לא רק הכירו את הפרופורציה של חתך הזהב, אלא גם היו מודעים לתכונותיה המתמטיות. אפלטון עצמו אף הסתמך עליהן בטיעוניו הפילוסופיים. “חיבורם של שני דברים בלבד״, אומר אפלטון, ״אי אפשר שיעלה יפה בלא משהו שלישי: שכן צריך שיהא ביניהם כבל מה שיקשרם יחדיו. ואין לך כבל נאה יותר מהמאחד איחוד מושלם ביותר את עצמו ואת כבוליו; ולפי טבע ברייתה, עשויה המתכונת הגיאומטרית להצליח מאין כמותה בכבילה מעין זו. שכל אימת שבתוך שלושה מספרים יהא המספר האמצעי בין שניים… עשוי כך, שכיחס הראשון אליו כן יחסו אל האחרון, ולהיפך: כיחס האחרון אל האמצעי, כן יחסו של זה אל הראשון כי אז, באשר האמצעי ייעשה ראשון ואחרון, והאחרון והראשון ייעשו שניהם אמצעיים, בהכרח שכולם יבואו זה במקום זה, (ואז) יהיו כולם לדבר אחד”. מחקרו החשוב של ארווין פנופסקי (Erwin Panofsky) “ההיסטוריה של התיאוריה של הפרופורציות של גוף האדם״1 מוביל למסקנה כי היוונים השתמשו בפועל בעיקרון של היחס של חתך הזהב לעיצוב פסליהם, ובוודאי גם ליצירות אמנות אחרות. בדיון על הקאנון הקלסי של פוליקליטוס מצטט פנופסקי את גאלן, המביא דברים מפי מלומד יווני ושמו קריסיפוס: “היופי אינו נובע מהאלמנטים אלא מהפרופורציה ההרמונית של החלקים: היחס של אצבע אחת לאחרת, של כל האצבעות לשאר היד, של שאר היד לפרק כף היד, של אלה לאמת היד, של האמה לזרוע כולה ובכלל, של כל החלקים לאחרים, כפי שכתוב בקאנון של פוליקליט״2
פנופסקי מציין כי הקאנון של פוליקליטוס (המודגם בצורה המושלמת ביותר בפסלו ״נושא הכידון” – תמונה 5), מושתת על עיקרון של פרופורציות ״אורגניות״ ולא, כמו הקאנון המצרי למשל, על עיקרון מודולרי סגור ונוקשה.
למעשה, העיקרון של הפרופורציה שהוא מכנה ״אורגנית” אינו אלא העיקרון של יחס חתך הזהב. לפי מחקרים 40מודרניים, עיקרון זה נפוץ ביותר במבנים צורנים שונים בטבע, החל בגוף האדם וכלה בצמחים וצדפות. כמו כן, אפשר להבחין בו כטור מתמטי ביסוד ההתפתחות המורפולוגית של צמחים ובעלי חיים.
הבנה נכונה של עובדה זו חשובה לדעתי לאין שיעור יותר מאשר הידיעה (הנפוצה מאוד מאז ויטרוביוס ואילך) בדבר היחס בין הראש (של הפסל) לשאר חלקי הגוף. לאור המשמעות האסתטית (ואפשר לומר שגם האורגנית) של הפרופורציה של חתך הזהב, אפשר להבין טוב יותר אימרה אחרת של פוליקליטוס, “היפה מופיע בהדרגה מבעד למספרים רבים״. כלומר, לפי הפרשנות של פנופסקי, הקאנון הקלסי של היפה מצוי “בתיאום של החלקים אלה לאלה ולשלמות”.
הרעיון בדבר הקשר בין המספרים ל״יפה״ נטוע עמוק במחשבה היוונית הקלסית. עבור אפלטון, למשל, “המספרים הם הדרגה הגבוהה ביותר של הידיעה״. יתרה מזו, לדעתו המספר הוא הידיעה עצמה. התפיסה ש״הכל הוא מספר” מקורה ככל הנראה בפיתגוראים, שסברו כי קיים קשר הדוק בין מספרים לבין צורות גיאומטריות. סברה זו איפשרה לעבור מתחום המחשבה אל תחום הממשות הוויזואלית, הלא הוא התחום בו היפה “נראה” במובן ההגליאני של הארה. ב׳׳טימאוס” פיתח אפלטון רעיונות אלה ותיאר את ארבעת ה״גופים״ (הצורות הגיאומטריות) של הבריאה, הנובעים כולם מסוג זה או אחר של משולש. כל אחד מהגופים הללו תואם לאחד מיסודות הבריאה: הקובייה = אדמה, התתראהֶדרון (פירמידה על בסיס של משולש) = אש, האוקְטָאהֶדרון (תמניון) = אוויר והאיקוֹסָאהֶדרון (עשרימון) = מים. גופים אלה מהווים, כדברי אפלטון, “מתכונת גיאומטרית״ או “דפוס דגם” גיאומטרי לכל הבריאה, כולל בעלי החיים והאדם.
הגיאומטריה כדפוס דגם של החיים
במרוצת הדורות ניסו אמנים רבים להמחיש את הגופים האלה בשירטוטים ובעיצוב תלת ממדי. השירטוטים הידועים ביותר הם אלה שהכין ליאונרדו דה וינצ׳י עבור ספרו של פאצ׳ולי (לוח 6). אלברט דירר שילב גופים גיאומטריים האמורים לייצג את יסודות הבריאה באחד מתחריטיו הנודעים – 41“מלנכוליה״ (1514, תמונה 7). מצד שמאל רואים דמות אשה מכונפת יושבת בתנוחה מהורהרת טיפוסית, ולימינה, במישור האמצעי של התחריט, בולט גוף גיאומטרי גדול מורכב מצורות ״אפלטוניות”. במישור הראשון, לרגלי האשה, מונח כדור יחסית קטן. והנה, הכדור (כמוהו כעיגול) הוא לפי אפלטון ״הצורה המושלמת ביותר והאחידה ביותר… המקפלת בתוכה את כל הצורות שישנן”. לכן הכדור (או העיגול) הוא צורת ״מבנה העולם” שהוא ״אחד מושלם״.
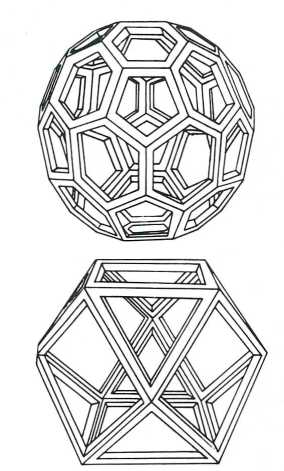

אולם, למרות היותו מסומן על ידי העיגול, ה״אחד המושלם” הוא מושג הניתן לחשיבה בלבד. יתר על כן, מוסיף אפלטון ב״טימאוס״, ״בתוך מצב של אחידות לא תיתכן תנועה… ובאין תנועה אין חיים״. לכן, מבנה העולם של החי מסומן על ידי הדודקאהדרון (תריסרון) המורכב מ-12 מחומשים והקרוב ביותר בצורתו לכדור. וכדברי אפלטון, ״עוד נשתייר מבנה אחד – החמישי, והאל השתמש בו לצורך הכל וקישטו בתמונות של בעלי חיים״.
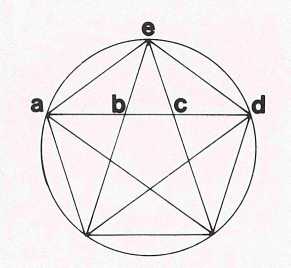
המחומש הוא הצורה הגיאומטרית המבוססת יותר מכל אחרת על היחס של חתך הזהב (לוח 8). לכן המחומש הוא הצורה המושלמת ביותר הבנויה על ״אי שוויון״.
לפי אפלטון, ״אי שוויון הוא הגורם לחוסר אחידות”. בהיותו קרוב ביותר לצורת העיגול, כלומר לאחידות מושלמת. הדודקאהדרון קרוב ביותר לאידיאה הנצחית של העולם; ובהיותו בנוי על עיקרון של אי שוויון הוא מביע מצב של חוסר אחידות, של תנועה, שהיא תנאי הכרחי לחיים. העיקרון של יחס חתך הזהב הוא אם כן זה המאפשר שילוב של אחידות ותנועה. משום כך זהו העיקרון של ה׳׳יפה” המושלם והנעלה ביותר שניתן לתפוס בחושים. בימי הביניים נשכח ההיבט הפילוסופי, אך נותרה אמונה בקדושה של מספרים מסוימים (שלוש, למשל) ושל צורות גיאומטריות מסוימות (בייחוד המחומש והכוכב הכלול בו), שיוחסה להם תכונה “אלוהית” של שלמות (ויופי). מספרים וצורות אלו (ובאמצעותם, כמובן, גם הפרופורציה של חתך הזהב) שימשו דגמים ליצירות רבות מאוד באדריכלות, בקישוט, בציור ובפיסול, ונמנו עם הסודות השמורים של סדנאות האמנים הביניימיים.
כאשר פירסם פאצ׳ולי את ספרו “הפרופורציה האלוהית”, הוא חשף למעשה את ה״סודות״ האלה וביטא מחשבה שהסתמכה על המקורות הקלסיים, לפיה המתמטיקה והגיאומטריה הן כלים ראשונים במעלה להשגת השלמות, ה׳׳יפה”, באמנות. כך, בלי שסילק את הילת הקדושה סביב חתך הזהב, הוא גילה את העקרונות הפילוסופיים והמתמטיים שלו באופן שעשוי היה לספק את רצונם של אנשי הרוח ואמני הרנסנס לבסס את מחקריהם על ידע ודאי ולא עוד על דעות מוכנות מראש.
עוד בתחילת המאה ה-15 הובע רצון זה בספרו של אלברטי (Alberti) “על הציור״: “אני מצפה שהצייר יהיה בקיא ככל האפשר בכל האמנויות הליברליות, אך יותר מכל אני רוצה שיהא בקיא בגיאומטריה״. היה זה רצון מובן ומוצדק, אם נזכור שהגיאומטריה היתה בסיס הפרספקטיבה, אותה המצאה כבירה של הרנסנס, שאיפשרה ליצור על משטח דו-ממדי אשליה של עולם מלא, תלת-ממדי. עם זאת חשוב להדגיש, כי הידע של המשמעות הפילוסופית של הצורות הגיאומטריות היה גם הוא חשוב ביותר לאמני הרנסנס. ואכן, הם השתמשו במשמעות הקלאסית של אותן צורות כבתשתית למשמעויות איקונוגרפיות-נוצריות של יצירותיהם. דוגמה אחת מני רבות היא הציור של פיירו דלה פרנצ׳סקה ״טבילת ישו״ (תמונה 9), המשלב (בפורמט ובקומפוזיציה) ריבוע, המסמל את האדמה, עם עיגול – סמל הבריאה כולה והאלוהות. במרכז הריבוע ניצב ישו – התגלות האלוהות עלי אדמות, ובדיוק במרכז העיגול מצויה היונה – המייצגת את רוח הקודש ואת האחדות האלוהית של השילוש הקדוש3 . מהמאה ה-16 ועד תחילת המאה ה-19 שוב נשכחו ההיבטים הפילוסופיים והאסתטיים של ״הפרופורציה האלוהית”. שוב שקע חתך הזהב בערפל של המיתוס כסמל מפוענח של “היפה״. אבל הוא הוסיף להתקיים בפועל, אם כי ללא מודעות של המשתמשים בו, באמצעות הליכים מקובלים בסדנאות אמנים, כגון מישבוץ ורשתות (Grids) מסוגים שונים.

חתך הזהב מחליף את הפרספקטיבה
המאה ה-19 מאופיינת בהתעניינות מחודשת בבעיות מדעיות-מתמטיות 42 של האמנות הפלסטית. חוקרים והיסטוריונים של האמנות מעלים מחדש את הדעה שאין ניגוד בין המתמטיקה והאמנות; הולכת ומתחזקת ההנחה כי חוקי היופי המסורתיים נובעים מעקרונות מתמטיים. הלוך רוח זה מתקשר עם גל של מחקרים, בייחוד של חוקרים גרמנים, על חתך הזהב.
החשוב שבהם היה אדולף צייזינג, אשר בספרו ״ביקורת מורפולוגית” (1863) ביקש להוכיח כי מספר הזהב הוא המפתח למורפולוגיה בטבע ובאמנות כאחד. המחקר הניסיוני הראשון בנושא חתך הזהב, שעשה גוסטב תיאודור פכנר, פורסם ב-1876. פכנר ניסה להוכיח באמצעות ניסויים בעלי אופי פסיכולוגי כי לרוב האנשים יש העדפה בולטת לפורמט של מלבן זהב. לקראת סוף המאה ה-19 מוזכר חתך הזהב בכתבים של המלומד הצרפתי שארל הנרי, שהיה לו קשר הדוק עם הציירים הניאואימפרסיוניסטים ג׳ורג׳ סרה ופול סיניאק4 . פול סריזייה, אחד הציירים הבולטים בחוג הנאבי5 שמע על חתך הזהב בעת ביקור אצל ידידו הצייר ההולנדי ורקאד (Verkade) במנזר הבנדיקטיני של ברון (Beuron) שביער השחור בגרמניה. במנזר זה ישבה קבוצה של נזירים-ציירים שביצעו לפי התיאוריה של האב לנץ קומפוזיציות דתיות (ויש לומר – קרות ומשעממות), מבוססות על “מידות קדושות״6 . גם סריזייה נשבה בקסמי התיאוריה, וב-1905 אף תירגם לצרפתית את ספרו של לנץ, ״האסתטיקה של ברון״. התלהבותו היתה כה גדולה, עד שלא החמיץ כל הזדמנות להסביר לידידיו הציירים את התכונות המופלאות של המספרים ובייחוד של חתך הזהב. אפשר להניח כי הצליח לעניין גם ציירים מחוג הקוביסטים, אשר לקראת סוף 1912 ערכו תערוכה שנקראה, ולא במקרה, ״חתך הזהב”. סדיזייה היה הראשון ששם לב לכך שהפורמטים 43המקובלים של תמונות הנמכרות בשוק מושתתים על פרופורציות של חתך הזהב. כך הגיע למסקנה, אותה העביר לתלמידיו, שאפשר לשרטט בקלות, בלי חישובים מסובכים ובעזרת שיטה גרפית פשוטה, רשת של קווים המבוססת על חתכי זהב, ולבנות עליה את הקומפוזיציה. תגלית זו היתה דבר בעיתו בתקופה שבה האמנים התרחקו מתיאור אשלייתי של המציאות ודחו את השימוש בפרספקטיבה. אבל הרשת הפרספקטיבית שירתה את האמנים לא רק כאמצעי ליצירת אשליה של עומק וחלל בציור, אלא גם כשלד בסיסי לאירגון נאות של הקומפוזיציה. דחייתה השאירה במובן זה חלל ריק. ברגע היסטורי זה סיפק חתך הזהב לציירים רשת חלופית, שהלמה את צורכיהם בהיותה חופפת למשטח התמונה, גם אם לא תמיד הכירו את טיבה המתמטי והאסתטי.
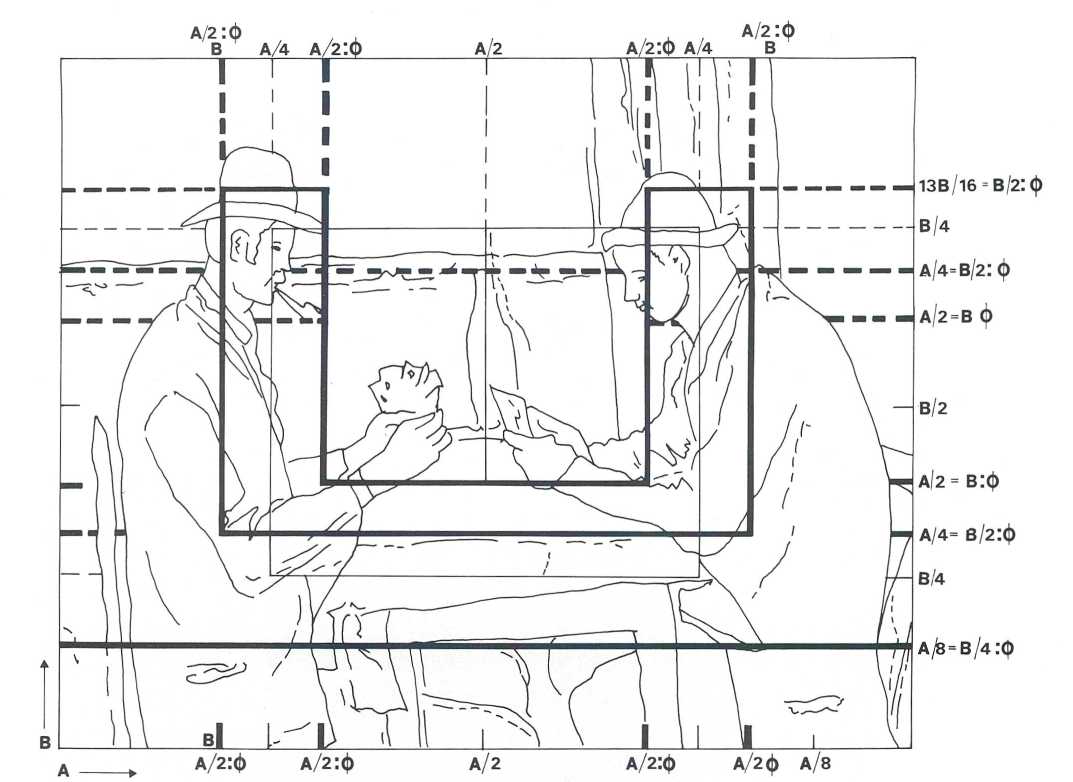
שימוש בסוגים שונים של רשתות היה מקובל גם קודם לכן, אך במחצית השנייה של המאה ה-19 שימשו רשתות שנגזרו מהפורמט עצמו של התמונה, ולקראת סוף המאה היה שימוש זה נפוץ יותר. בהסתמכם על רשתות כאלו בחרו האמנים, בדרך כלל שלא בכוונה תחילה, בקווים חופפים לחתכי הזהב ובנו, כמו סזאן למשל, קומפוזיציות מאוזנות אך טעונות מתח (תמונה 10). בזמננו משתמשים אמנים בחתך הזהב תוך מודעות מלאה לסגולותיו ולעיתים בצורה מורכבת ומתוחכמת ביותר. יעקב אגם אמר לי במפורש כי הוא משתמש בעבודותיו במיקצבים המבוססים על פרופורציות של חתך הזהב, שאת מירווחיהם הוא בוחר בעזרת מחשב. מסתבר שכמו בתקופת הרנסנס, מתעניינים אמנים רבים בני ימינו בחתך הזהב הן בזכות תכונותיו השימושיות והן בשל המשמעות הסמלית (ואפשר לומר מיתית) שלו. בדרך כלל נשענת התעניינותם על ידיעה והבנה: ידיעה של העיקרון המתמטי (פרופורציה פתוחה, לא מודולרית, הטומנת בחובה אינסוף אפשרויות) והבנה של המהות הפילוסופית (פרופורציה המגלמת במסגרת אחדותית תחושה של תנועה וחיים).
אמנים בני זמננו
פתחתי בשני אמנים בני זמננו, ששילבו בעבודותיהם נוסחה מתמטית של חתך הזהב או מספרים ברצף של טור פיבונצ׳י כמסמנים של היפה, ואסיים בשתי עבודות של אמנים איטלקים מודרניים, שבאמצעותן אבקש להצביע על ההתאמה בין מבנה הקומפוזיציה לבין מבחר של חתכי זהב.
העבודה הראשונה, “קונספט מרחבי – ציפיות” (1959, תמונה 11א) של הצייר44 לוצ׳יו פונטנה, היא תמונה “מתמטית” הבנויה בחיסכון רב של אמצעים: שני צבעים מנוגדים בעוצמתם, ארבעה חתכים ממוקמים על שני קווים (לא נראים) החוצים את הבד לגובהו, כמה פסים אופקיים בעלי עובי שונה ובמרחקים לא שווים זה מזה. הסידור – לא סימטרי ולכאורה פשוט ביותר. התבוננות ממושכת ומעמיקה מגלה, כי למרות מיעוט האלמנטים ופשטותם, יש בתמונה מורכבות גדולה. התאמה של רשת חתכי זהב לפורמט של התמונה מראה שיש חפיפה מלאה ביניהם לבין שני חתכי זהב לא סימטריים של הפורמט (לוח 11ב’) וכן בין הפסים האופקיים לחתכי זהב אחרים. המירווחים והמיקצבים של הפסים האופקיים נשענים על יחסים אופייניים לחתך הזהב, כלומר יחסים שיש בהם בו זמנית יסודות של סדר ושל אי סדר מסוים. אפילו החתכים בבד, האמורים להיות מיחוותיים-ספונטניים, נופלים בדיוק, ואפשר להניח שלא במקרה, על חתכי הזהב.


הדוגמה השנייה – עבודה של אלברטו בורי משנת 1952 המכונה “שק”, המורכבת מחתיכות שק תפורות יחדיו בתפרים גסים. הצבעים – מבחר של אוקרים וחומים בהירים כנגד לבן-קרמי בהיר וחום כהה (תמונה 12א). מה יכול להיות דל מזה כחומר ופשוט יותר, לכאורה, כמבנה? בכל זאת, יש בתמונה זו משהו מושך שגורם לנו נחת, משהו שאנו מזהים אותו עם המושג של ה׳׳יפה”. ייתכן כי תחושה זו נובעת מההרמוניה של הצבעים, אך לא רק ממנה. אם נלביש גם על תמונה זו רשת של חתכי זהב, ניווכח שגם בה יש חפיפה מפתיעה ביניהם לבין הקווים העיקריים של הקומפוזיציה (לוח 12ב).


בהעדר עדות ברורה ומוסמכת נשארת פתוחה השאלה, אם אמנם תיכננו האמנים את תמונותיהם ובנו אותן על סמך רשת מסוימת של חתכי זהב. אין להוציא מכלל אפשרות מצב שהוביל אותם, על סמך הליכים פשוטים ושגרתיים, אך מתוך נטייה פנימית אמיתית, לבניית קומפוזיציה הרמונית, תולדת סדר ושלמות, המחזיקה בתוכה ערכים של אי סדר (אי שוויון, לפי אפלטון), המולידים תנועה וחיים. אבל, עצם העובדה שביצירות כה רבות קיימת התאמה מופלאה בין הקווים העיקריים של המבנה לבין חתכי הזהב הנגזרים מהפורמט, מוכיחה גם היא שיש קשר אמיץ בין הפרופורציה של חתך הזהב ובין מושג ה׳׳יפה”. ■45
Erwin Panofsky, “The History of the Theory of Human Proportions as a Reflection of the History of Styles”, In Meaning in the Visual Arts, Anchor Books A59, USA 1955 ↩
שם, עמ׳ 64 ↩
יש לציין כי החלק התחתון של הציור אינו ריבוע מושלם, אך דבר זה אינו משנה לגבי המשמעות. מעניין לשים לב לעובדה שהעיגול כולל את החלק העליון של גופו של ישו ומשייכו לתחום הרוח, בעוד החלק התחתון שייך לתחום החומר בלבד (כאדמה). ↩
יש סברה שג׳ורג’ סרה (Seurat) הסתמך ביצירותיו על חתך הזהב הודות לידע שרכש באמצעות שארל הנרי. ↩
קבוצת ה-Nabis (נביאים) נוסדה בפריס לקראת סוף המאה ה-19 על ידי כמה אמנים צעירים והטיפה לחזרה לנצרות ולקלסיציזם. בסגנונם הושפעו מגוגן, סזאן ומחיתוכי עץ יפניים. היו קרובים לסימבוליזם ולסגנון של אר-נובו (Art Nouveau) שאיפיין את המעבר בין שתי המאות. ↩
האב לנץ פיתח תיאוריה, לפיה כל היצירות הגדולות של העבר ובעיקר של מצרים העתיקה נעשו בהתאם למספרים (קדושים) ביחסים מוגדרים (עם עדיפות ראשונית ליחס של חתך הזהב). ↩







