הנבון המחשב?

הקדמה:

נחמן גבעולי הוא בוגר הפקולטה למתימאטיקה-פיסיקה באוניברסיטה העברית בירושלים. עסק בהוראת מקצועות אלה בגימנסיות בתל-אביב וברמת-גן, וכיום מכהן בתור התוכניתן הראשי של בנק לאומי לישראל. מר גבעולי משמש גם כעורך המדור ״חידות ושעשועים מתימאטיים” של כתב-העת ״מדע״.

המסוגל המחשב לחשוב בצורה נבונה? שאלה זו כבר עוררה ויכוחים רבים; הן לגבי עצם התשובה והן לגבי המסקנות הנובעות ממנה — כאשר התשובה חיובית. האם עשוי המחשב להצר בעתיד את צעדי האדם ולגזול את מקומו כבעל חזקה על מושג התבונה? אם נטיל על מכונות את פעולת החשיבה, כשם שהטלנו עליהן את הפעולות שהצריכו עמל גופני — האם לא עלול הדבר להשפיע על התפתחות האנושות?

בגליון ספטמבר של הירחון ״סייאנטיפיק אמריקן״, המוקדש הפעם כולו למחשבים, פיתוחם כיום וסיכוייהם לעתיד, מופיע בין היתר מאמר מאת פרופ׳ מרוין ל. מינסקי, איש מ.י.ט. (מכון מסצ׳וסטס לטכנולוגיה), המתאר כמה עבודות-תיכנות, ״המאפשרות למחשב לפעול בצורה, אשר בוודאי תיראה נבונה לכל אדם״. (ההדגשה שלי — נ.ג.)

פרופ׳ מינסקי מניח, אולי בצדק, כי תיאור פעולות אלו של המחשב מהוות, מעשית, הוכחה מספקת לתבונתו. אולם הויכוח בשאלה זו הוא עקרוני יותר משהוא מעשי. עד היום, כשאתה משוחח עם אדם בענין זה, עלול אתה להיתקל בתגובה מעין זו: עם שהוא מוכן, אמנם, להודות שהמחשב מסוגל למיבצעים מפליאים, ימהר עם זאת לציין, שמבצעים אלה עדין אינם נחשבים בעיניו כגילויים של תבונה ממש. הדעה המקובלת היא — לפחות בין אנשים שאינם עוסקים בפועל בחקר תחום זה — שקיימת תכונה אינטלקטואלית יסודית, אשר היא ״מותר האדם מן המחשב״, ותהום זו ביניהם לעולם לא תהיה ניתנת לגישור.

מהי אותה תכונה אינטלקטואלית מסתורית? שאלה זו נשאלה כבר ע״י החוקר א. מ. טיורינג, במאמר שהופיע בשנת 1950, בכתב העת הפילוסופי ״מימד״, והנחשב היום כקלסי בתחום זה. טיורינג מונה טענות רבות שנטענו ונטענות נגד ייחוס תבונה למחשבים, ומבטל את כולן. חלק מהטענות שהוא מזכיר אין להן משקל רציני, והן נובעות בצורה שקופה מכך שהשואל מתקומם נגד הרעיון באורח אמוציונלי — אם מסיבות של אמונה דתית, או מתוך גאוה עצמית שנפגעה, או מתוך שמרנות מחשבתית גרידא. חלק אחר של הטענות נגד אפשרות של תבונה במחשבים מצביע על מגבלות, שהן, למעשה, פונקציה של קיבולת הזכרון של המחשב. טיורינג מוכיח כי תכונות, כגון: רב-גוניות, למידה עצמית ועוד, ניתנות להשגה במחשבים, בתנאי שקיבולת זכרונם תהיה גדולה למדי. במשך 16 השנים שעברו מאז נתאשרו דבריו אלה. אולם קיימת גם קבוצה שלישית של טענות, עקרוניות יותר, המבוססות על עצם ההגדרה של מושג החשיבה. טיורינג מציין, כי תמיד תיתכן מחלוקת בשאלה אם מכונה מסוגלת לחשוב, כל עוד לא נסכים בינינו סופית מהי בדיוק חשיבה. מאחר שאין כל בטחון שנגיע אי פעם להסכמה לגבי ההגדרה של מושג זה, הריהו עוקף את הבעיה ואת הויכוחים הפילוסופיים הכרוכים בה, ומציע שיטת מבחן מעשית.

שיר על האביב

מבחנו של טיורינג הוא פשוט למדי: כדי להשיב על השאלה אם מסוגלת מכונה לחשוב כבן אדם, נציג את השאלה בצורה אחרת: האם יכולה מכונה להשיב לשאלותיו של בוחן בצורה כזו, שהוא לא יהיה מסוגל לקבוע אם אדם הוא המשיב, או מכונה? אם תצליח11 בכך, נהיה נאלצים להודות, כי המחשב מסוגל לחשוב כבן אדם. שהרי, אם א׳ מסוגל לחקות בהצלחה את פעולותיו של ב׳, אין לנו ברירה אלא להסכים כי א׳ אינו נופל מ-ב׳ בפעולות אלו.

נושיב, איפוא, את הבוחן בחדר שבו נמצא טלפרינטר, הקשור לחדר סמוך. בחדר הסמוך יכול להימצא מחשב, או אדם. הבוחן שואל שאלות באמצעות הטלפרינטר, ומקבל דרכו את התשובות, ועליו לקבוע אם המשיב הוא מכונה או בשר ודם. הבוחן, כמובן, רשאי לנסות להפיל את הנבחן בפח באמצעות שאלותיו, ודווקה שאלות מתחום הרגש והרוח, שהרי בשאלות חישוביות עדיף המחשב מן האדם. הרי דוגמה של מבחן המופיעה במאמרו של טיורינג:

הבוחן: חבר שיר על האביב. הנבחן: הנח לי. מעולם לא ידעתי לכתוב שירים. הבוחן: כמה הם 70764 ועוד 34957? הנבחן: (לאחר שהייה של 30 שניות): 105721. הבוחן: מונח לפני שיר המתחיל במלים, ״האם אשווה אותך ליום אביב״? האם אי אפשר היה לכתוב במקום זה ״ליום קיץ״ ?

הנבחן: המשקל אינו מתאים.

הבוחן: ומה בדבר ״ליום של סתו״?

הנבחן: איש אינו רוצה להיות מושווה ליום של סתו.

טיורינג אינו מנסה להוכיח מראש, כי מחשב יוכל אי-פעם לעמוד בכל מבחן מסוג זה בהצלחה. מאחר שהמבחן הוא כה כללי, הרי קשה להאמין שניתן למצוא הוכחה תיאורטית לכך שיכולים אנו, בפוטנציה, לבנות מחשבים כה מוכשרים. עם זאת אין טיורינג מהסס להביע את אמונתו, כי תוך 50 שנה יסכימו כולם לכך שהדבר אפשרי!

טיורינג היה סבור בשנת 1950, כי עד סוף מאה זו ייבנו מחשבים בעלי תפוסת זכרון של ביליוני תאים, וייכתבו להם תכניות המסוגלות לעמוד במבחנו בהצלחה רבה למדי. אם בשנת 1950 היה המושג ״מכונות חושבות״ מעורר ויכוחים, הרי עד סוף המאה, כפי שהאמין טיורינג, יסתגלו אנשי המקצוע לרעיון במדה כזו, שהוא יתקבל כמובן מאליו — הן הודות לשכלול המחשבים, והן הודות להבהרת מושג החשיבה. טיורינג נפטר באורח פתאומי כעבור ארבע שנים, אך אילו חי עכשיו אין להניח שהיה מוצא צורך לשנות את דעתו. ההישגים שהושגו בשנים האחרונות, והאופקים החדשים שנפתחו, תומכים בדעתו, אם-כי עדיין רחוקים הם ממימוש מטרה זו.

המבחן הפסיכוטכני

 

במאמרו ב״סייאנטיפיק אמריקן״ מספר פרופ׳ מינסקי על קבוצה של חוקרים שנתקבצה בשנת 1956 לעיין באפשרות של בניית מחשבים ״נבונים באמת״. על קבוצה זו נמנו, מלבד מינסקי עצמו, כמה תוכניתנים שכבר התנסו בתכניות חשיבה: ארתור ל. סמיואל, איש י.ב.מ., שכתב תכנית המסוגלת לשחק ב״דמקה״ וללמוד מנסיונה; ניואל, שאו וסיימון, שכתבו תכנית המסוגלת להוכיח משפטים בלוגיקה וכן תכנית כללית לפתירת בעיות בשיטה של ניסויים והצבת מטרות-ביניים. מינסקי עצמו כתב כבר תכנית המוכיחה משפטים בגיאומטריה.

כתוצאה מאותה פגישה נטלה על עצמה קבוצתו של פרופ׳ מינסקי, המורכבת מבוגרי מ.י.ט., לכתוב תכניות המסוגלות לפתור בעיות בדרך ״אינטואיטיבית״, כביכול. מינסקי אינו קורא לדרך זו ״אינטואיטיבית״, אלא ״הייריסטית״. הכוונה לתכנית הבוחרת לעצמה את הכיוון שבו תחפש את הפתרון, והיא עושה זאת לא על סמך בדיקות שתוצאותיהן ודאיות, אלא על סמך השערות וגישושים, בדומה לאדם המהפך במוחו אפשרויות שונות ומנסה כה וכה לפתור בעיה כלשהי. אחת הדוגמאות שמינסקי מביא, היא תכנית המסוגלת לעמוד במבחן פסיכוטכני, מסוג מבחני הציורים המקובלים, המציגים שלושה ציורים, א׳, ב׳, ג׳. המבחן הוא לבחור בציור רביעי, ד׳, המתיחס לציור ג׳ באותו אופן שבו מתיחס ציור ב׳ לציור א׳. נניח שציור א׳ הוא מעגל, ציור ב׳ — אליפסה, וציור ג׳ — ריבוע. מאחר שאליפסה היא כעין מעגל מאורך, הרי ציור ד׳ צריך להיות מלבן, שהוא כעין ריבוע מאורך. למעשה אין הנבחן צריך להמציא את ציור ד׳ מדמיונו, אלא לבחור בו מתוך 5 אפשרויות נתונות.

כתיבת תכנית המסוגלת לעמוד במבחן כזה, היא קשה ומענינית במיוחד, מכמה סיבות. ראשית, הכרת צורות היא עד היום אחת מנקודות התורפה של המחשב. ידוע כמה קשה לבנות מחשב שיוכל לקרוא כתב יד, או אף אותיות דפוס, אם אין אלו אותיות במבנה קבוע ומוגדר מראש. שנית, במקרים רבים הבחירה של ציור ד׳ אינה חד-משמעית. הנבחן אינו נדרש למצוא את התשובה היחידה האפשרית, אלא את התשובה המתאימה ביותר. שלישית, כדי לקבוע את ציור ד׳ חייב הנבחן לערוך השוואות ולנסח אנלוגיות בין צורות, ולגבי מחשבים תפקיד זה הוא חדש.

מינסקי מעיר, כי למרות שמבנה התכנית היה מוכר לחוקרים, הרי עד שניסוה מעשית לא היה להם כל מושג באיזו מדה תוכל להתחרות בנבחן בשר ודם. הרי זו שוב הוכחה לכך, שהמחשב יכול בהחלט להפתיענו בהישגיו. מסתבר שהתכנית מסוגלת להתחרות בהצלחה בתלמיד הכתה השישית של גמנסיה, אך לאחר שיכניסו בה שכלולים מסוימים יש להניח שרמתה עוד תשתפר.12 הבעיה מוזנת למחשב בצורת נתונים מספריים, המגדירים נקודות, קוים ישרים ועקומים, שטחים וכו’. התכנית מפרקת כל ציור למרכיביו, ורושמת לעצמה את היחסים בין המרכיבים, היינו, את המיקום ההדדי שלהם. לאחר מכן היא מחפשת שיטה, שלפיה אפשר לקבל מציור א׳ את ציור ב׳. יתכן שהתכנית תצטרך להביא בחשבון יותר משיטה אפשרית אחת. בשלב הבא היא מוצאת את כל המרכיבים המשותפים ל-א׳ ול-ג’, ומנסה לפעול על מרכיבי ג׳ באותה השיטה בה שונו מרכיבי א׳. היא מחפשת בין האפשרויות הנתונות לתשובה את התוצאה הרצויה לה, או ציור הדומה יותר מכל האחרים לתוצאה הרצויה.

בניית משוואה ממשפט רגיל

חוקר אחר מקבוצתו של פרופ׳ מינסקי כתב תכנית, שתפקידה לפתור בעיות אלגבריות פשוטות למדי. האתגר במקרה זה אינו במידת הסיבוך של הבעיות עצמן, אלא בעובדה שהבעיות מוזנות לתכנית באנגלית רגילה. לצורך זה ניתנה לתכנית גישה למילון של מלים, מושגים וכללי דקדוק. ברור שמילון זה הוא בהכרח מצומצם למדי, וכפי שנראה בדוגמאות דלהלן, אין הוא מכיל את כל צירופי המלים שהתכנית עלולה להיתקל בהם. בכל מקרה של מושג בלתי מוגדר, מנסה התכנית לשער בעצמה את מובנו המדויק, או לשאול שאלה כדי להבהירו. במקרים רבים חוסר הבהירות אינו נובע ממלה החסרה במילון, אלא מניסוח לא מדוייק של הבעיה, כפי שנראה בדוגמאות הבאות.

בעיה א’.

צריכת הדלק של מכוניתי היא 15 מיל לגלון. המרחק בין בוסטון לניו יורק הוא 250 מיל. מה הוא מספר הגלונים של דלק הדרוש לנסיעה בין ניו-יורק לבוסטון?

התכנית אינה מבינה, אך גם אינה צריכה להבין, את פירוש המלים ״מכוניתי״, ״בוסטון״ וכו׳; אך היא מכירה את הנוסחה דלקמן:

(מספר הגלונים הדרוש) = (המרחק) x (צריכת הדלק)

שלושת המונחים המשתתפים בנוסחה נזכרים בשאלה תוך שינויים קלים במלים, ולכן התכנית מעירה כי היא נאלצת להניח הנחות מסוימות : המרחק = ״המרחק בין בוסטון לניו-יורק״. צריכת הדלק = ״צריכת הדלק של מכוניתי״. מספר הגלונים הדרוש = ״מספר הגלונים של דלק הדרוש לנסיעה בין ניו-יורק לבוסטון״.

לאחר שהניחה את ההנחות הללו מודיעה התכנית את התשובה הנכונה.

בעיה ב׳.

המשקל ברוטו של ספינה הוא 000 20 טון. אם משקלה נטו 000 15 טון, מה הוא משקל מטען הספינה?

במקרה זה אין התכנית יודעת נוסחה הנוגעת לנתונים אלה. לכן היא שואלת :

״האם ידועה לך נוסחה המקשרת בין ״המשקל ברוטו של הספינה״, ״טון״, ״משקלה נטו״, ״משקל מטען הספינה״ ?

שוב, התכנית אינה מתענינת במובנם של מונחים אלה, אלא רק בקשר המאתימאטי ביניהם. כשמודיעים לתכנית כי — משקל מטען הספינה שווה להפרש בין המשקל ברוטו והמשקל נטו, היא מוסיפה עובדה זו לאוסף הנתונים שלה, אך שוב נאלצת היא להניח הנחות מסוימות:

המשקל נטו = “משקלה נטו״.

המשקל ברוטו = ״המשקל ברוטו של הספינה״.

גילוי של אינטואיציה

כשרון האינטואיציה בא, אולי, לידי הביטוי הבולט ביותר בתכנית אחרת, אף היא של איש מ.י.ט., ואף היא נכתבה, כמו שתי הקודמות, במסגרת עבודת דוקטורט. תכנית זו ״מתבוננת״ בצילום של גוף גיאומטרי כלשהו, כגון פריסמה מחומשת, ועל סמך תמונה זו היא מסוגלת לצייר תמונה של אותו גוף, כפי שהוא נראה מזוית אחרת, לפי המבוקש. נוכל להיווכח עד כמה מפליא הישג זה אם נזכור, כי אדם הניצב לפני אותו תרגיל, מסתמך על נסיון עשיר של ראיית גופים מזוויות שונות. כשאדם רואה צילום של קוביה, למשל, מה בעצם אומר לו שזוהי תמונה שטוחה של גוף תלת-מימדי? בעיקר — ההבדלים בתאורה של המשטחים השונים. אך נסה לפרט במלים את התהליך המחשבתי שלפיו אתה יודע כיצד תיראה קוביה זו מזוית ראיה אחרת!

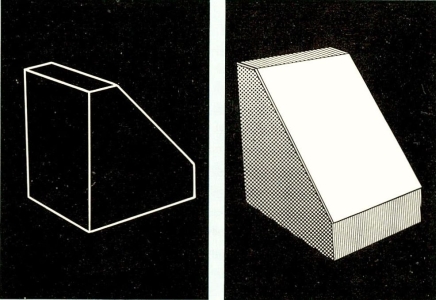
תכנית שפותחה ב-מ.י.ט. מאפשרת למחשב לשנות את זוית ההצגה של גוף גיאומטרי (ראה תמונה) לכל זוית נדרשת. הדבר נעשה בכמה שלבי ביניים המפרקים את התמונה הדו-מימדית לחתכים תלת-מימדיים (תיבות ישרות-זוית ופריסמות משולשות), עד להרכבתה מחדש בזוית המבוקשת.

פרופ׳ מינסקי אינו נותן במאמרו תיאור מפורט של תהליך מחשבתי זה מצד התכנית, אלא מסתפק בכך שהוא מציין כי התכנית מפרקת את הגוף לחלקים יסודיים, שהם תיבות ישרות-זויות ופריסמות משולשות, ועל סמך הרכב זה היא בונה אותו מחדש באוריינטציה הנדרשת.

פרופ׳ מינסקי מסיים את מאמרו באמרו, כי כדי שתכנית תוכל לקדם את עצמה במובנו האמיתי של מושג זה, ולא רק ללמוד להימנע משגיאות, עליה להכיר את תהליך החשיבה שלה עצמה ואת הכללים הלוגיים לפיהם היא פועלת, ואז תוכל להכניס בהם שיפורים.

בתחום זה אין עדיין אלא התחלה בלבד. הקשיים13 נובעים בעיקר ממגבלות בגודל הזכרון ומהסיבוך הכרוך בכתיבת תכניות כה משוכללות, אך אין אלה קשיים עקרוניים. לאחר שתחול התקדמות ניכרת בתחום זה, יתחילו הענינים להתגלגל במהירות, והתכניות תיעשינה יותר ויותר נבונות. אווילי הוא להניח, מסכם פרופ׳ מינסקי, כי המחשב יגיע פעם לדרגת תבונה רק כמעט כמו האדם, ושם תיעצר התקדמותו. המשפט האחרון במאמרו ראוי לציטוט מילולי:

״בין אם נוכל להמשיך ולשלוט במכונות, בהנחה שאמנם נרצה בכך, ובין אם לא נוכל, ישתנה לחלוטין אופי התנהגותנו ושאיפותינו, לאור נוכחותם עלי אדמות של יצורים העולים עלינו בתבונתם״.

ספקות וסייגים

בספרו ״אוטומטים — סיכויים וסייגים״ (ספרית הפועלים, 1964), מביע פרופ׳ יהושע בר-הלל דעה שהיא, לכאורה, מנוגדת לדעותיהם של טיורינג ומינסקי בצורה קוטבית. כבר-סמכא בתורת הקיברנטיקה, וכמי שעסק מעשית בבעיות של יישום המחשב לתפקידי מחקר בלשני ותרגום משפה לשפה, רב משקלן של מסקנותיו הפסימיות. כבר בפתח דבריו מזהיר הוא מפני אשליות שמחזיקים בהן חוקרים אחרים בנדון זה. ברם, תוך המשך העיון בספרו (שהוא, אגב, מרתק הן בתכנו והן בסגנונו המבריק), מתברר כי הניגוד בינו לבין הדעות שהובעו לעיל אינו כה חריף. לאחר שהוא דן בתכניות פשוטות, ומציג את מגבלותיהן, הריהו מפתח בהדרגה את הרעיונות הכרוכים בהתגברות על מגבלות אלו, היינו, באמצעות תכניות הלומדות מעצמן, תכניות הייריסטיות וכדומה, תוך שהוא מכיר בכך שרעיונות אלה ניתנות למימוש. הוא מסכם באמרו כי, בעוד ש״המחשבים מסוגלים לפתור כל בעיה, שאת האלגוריסמוס לפתרונה (היינו — דרך פתרון בדוקה — נ.ג.) אפשר להזין להם בשפה המובנת להם״, הרי רק לגבי מספר מוגבל מאד של בעיות ״אפשר לתלות תקוות של פתרון בעזרת תיכנות הייריסטי. לגבי אותן הבעיות, שהאדם פותרן על סמך נסיון חיים, ידיעות כלליות ומקצועיות — מתוך הבנה ולמידה המתבססות על ארגון סגולי מלידה של מערכת העצבים שלו — אין כרגע כל תקווה של ממש כי ייפתרו ע״י מחשבים״. אם נשים דגש על המלה ״כרגע״, יתכן שלא יהיה ויכוח בין בר-הלל לבין טיורינג. גם האחרון ציין במאמרו, כי אותו ״על-מחשב״ שיווצר אי-פעם, אינו חייב להיות דומה במבנהו למחשבים הקיימים היום, עד כדי כך שיתכן כי יהיו אנשים שלא יסכימו לקרוא לו בשם ״מחשב״ או ״מכונה״ בכלל. בדברים אלה מרמז הוא על האפשרות שבעתיד נלמד לייצר (או אולי ״לגדל״ היא המלה הנכונה) מוחות אורגניים, המורכבים מתאים חיים. הצורך בכך מסתבר גם מתוך דבריו של פרופ׳ בר-הלל, המציין את יתרונות שיטת הארגון של מערכת העצבים שלנו לעומת מבנה הזכרון ומעגלי הזרם של המחשב, לצורך פעולות אינטלקטואליות, כגון למידת שפה או משחק יעיל בשחמט. גם בלי להזקק לפעולות ברמה כזו, אפשר להראות כי מבנה מוחנו עולה ביעילותו, עקרונית, על זה של המחשב: אדם יודע, בידיעה שלמה ומיידית, כמות עצומה של אינפורמציה. נשאלת השאלה, כיצד הוא יכול ״לגשת״ לכל פריט בזכרונו במהירות כה גדולה, עד שהדבר נראה לנו כפעולה מיידית! אילו רצינו לאחסן כמות כה גדולה של אינפורמציה בזכרון המחשב, היינו עומדים בפני בעיה חמורה של ארגון, והזמן הממוצע הדרוש לאיחזורו של כל פריט היה בהכרח פונקציה ישירה של כמות החומר. אין לנו מושג כיצד מאורגן החומר במוחנו, וכיצד מתבצעת בו פעולת האיחזור. מסתבר, איפוא, שבנקודה זו עדין לא עלינו כלל על הפסים הנכונים, והמוחות המלאכותיים הם נחותים במידה יסודית לעומת מוחותינו הטבעיים בתחום קריטי זה.

ברם, גם אם נוריד את השאיפות שלנו לרמה צנועה הרבה יותר מחזונו של טיורינג, נשאלת עדייו השאלה אם יכול מחשב לגלות תבונה בתחום מצומצם שמועידים לו. יתכן שגם מינסקי לא נתכוון לטעון, כי אותן תכניות אשר תשפרנה את עצמן יותר ויותר, תהיינה מסוגלות בסופו של דבר, כל אחת בנפרד, לעלות בתבונתן על האדם. הכוונה היא, אולי, ״רק״ לכך, שכל התכניות האפשריות ביחד תהיינה נבונות מבני האדם. אם נאמר, שכל מחשב, או ליתר דיוק, כל תכנית, יהיה לה תחום פעולה משלה, ובתחום זה בלבד יהיה עליה לגלות את יכולתה, האם גם אז יהיו תמיד תחומים שבהם לא יוכל המחשב להגיע לרמתו של האדם?

איכות וכמות

פרופ׳ ישעיהו ליבוביץ׳, בהרצאתו בכנס רואי החשבון שנערך באוקטובר השנה, מביע את דעתו באותה הבעיה, שהיא שלילית אולי יותר מזו של פרופ׳ בר-הלל. אם-כי מבקש הוא שנביא בחשבון, כי גישתו היא ״גישה של חובב, שהתענין בדברים אלה, ואולי גם רשאי לומר שלמד אותם, אבל אין לו גישה מעשית אליהם״, הריהו מביא הגדרות מענינות להבדל שבין דרך מחשבתו של אדם לזו של מחשב, ולמעשה לגבי מחשב אין הוא קורא לכך חשיבה, אלא חישוב. ״כל דבר הניתן לביטוי בקטגוריה כמותית ניתן להציגו ע״י מודל מכני״, והודות לכך ניתן ליישמו למחשב; ואילו ״עד שאדם מגיע להצגת שאלה בקטגוריות כמותיות, הוא צריך לחשוב עליה״, היינו קודם-כל מבחינה איכותית (ההדגשות שלי — נ.ג.). המחשב מוגבל, איפוא, לפעולות חישוב, הדורשות הצגה כמותית. אם נסכים עם פרופ׳ ליבוביץ׳, נשאלת שוב השאלה, אם באורח עקרוני קיים תחום שאותו לא נוכל לעולם לבטא בקטגוריות כמותיות. אנו חוזרים, איפוא, לשאיפה ״הצנועה״ יותר ואומרים: — אם גם לא נוכל לעולם לבנות מחשב (או תכנית) אחד, שיהיה חכם מן האדם, האם ישנו תחום ספציפי שבו לא יוכל מחשב להתחרות עם בני האדם? כשם שבעבר העברנו יותר ויותר נושאים מפסים איכותיים טהורים לפסים כמותיים, כך יתכן שנעשה זאת גם לגבי יתר הנושאים, כגון כלכלה, מלחמה, בלשנות, אמנות וכו׳. האם חייב להשאר נושא שאותו לא נוכל לעולם להעביר למחשב? אולי, בסופו של דבר, הפעולה היחידה שתשאר תחומם הבלעדי של בני האדם, תהיה עצם פעולת הפורמליזציה הזו, היינו העברת נושא חדש כלשהו לפסים כמותיים. ענין זה קשור בהבדל אחר שמזכיר פרופ׳ ליבוביץ׳ בין דרך מחשבתו של האדם לזו של מחשב: המחשב מסוגל להשיב, אך אינו מסוגל לשאול. במאמרו של מינסקי מוצאים אנו לכאורה דוגמה של מחשב השואל שאלות, אך אלו הן שאלות שהוא חייב לשאול, כדי שיוכל להשיב על הבעיות המועמדות בפניו. לעולם אין הוא שואל ״סתם״, מתוך סקרנות, היינו שאלות ביזמתו שלו. ברם, אם נגענו בענין הסקרנות והיזמה, שהן חלק מענין רחב יותר — ההכרה — הרי הגענו לבעיות אשר אותן בדיוק רצה טיורינג לעקוף בעזרת המבחן שלו. • •14