הקדמה:
המאמר המתפרסם כאן עובד על פי מאמרם של J. Nievergelt ו־ J.C. Farrar מאוניברסיטת אילינוי, אשר ראה אור ביוני 1972, בגליון 2 (כרך 4) של ACM — Computing Surveys. המאמר מתפרסם ברשותם האדיבה של The Association for Computing) ACM Machinery).
במקורו התפרסם המאמר תחת השם: What Machines Can and Cannot Do והוא כלל פרק שלישי שדן במגבלותיהן הלוגיות של מכונות. פרק זה הושמט מטעמים טכניים. שני הפרקים המתפרסמים כאן עובדו על ידינו באותם מקומות שהיה חשש כי לא יובנו על ידי קהל הקוראים הלא מקצועי. קוראי ״מחשבות״ ימצאו ענין בהשוואת גישתם של מחברי המאמר בשאלת האינטליגנציה של מכונות עם גישותיהם של פרופ׳ ישעיהו ליבוביץ ופרופ׳ יהושע בר הלל — כפי שבאו לביטוי בגליונות קודמים של ״מחשבות״.

השאלה המעורפלת ״מה יכולות מכונות לעשות ומה אין ביכולתן לעשות״ עוררה פולמוס נרחב בעבר, וממשיכה להוות מקור מבוכה גם בהווה.
במשך 40 השנים האחרונות נוסחו מספר שאלות מדויקות למדי בנושא זה, אשר תרמו לא מעט להפרכתן של ״אגדות״ שקנו להן מהלכים. מאמר זה דן בשתים מבין שאלות אלו:
היכולה מכונה לחשוב ?
היכולה מכונה ״להכפיל״ את עצמה ?
השאלה ״מה יש ביכולתן של מכונות לבצע ומה אינן יכולות לבצע״ נשאלה לראשונה לפני היות המחשבים. למן לידתה של הטכנולוגיה היה האדם סקרן לדעת עד אנה תוליכו וגם לפניה חלמו ממציאים על מכונות המסוגלות להכפיל ולשלש את היכולת האנושית או להתגבר על מגבלותיה. אך עד היום אין תשובה יחידה וברורה לשאלה זו, ולו רק בשל כך שהמלים ״יכולות לבצע״ ניתנות לפירושים שונים. עם זאת, נוסחו ב־40 השנים האחרונות מספר שאלות שהדיון בהן פיזר לא במעט את הערפל הראשוני.
היכולה מכונה לחשוב?
״האם יכולה מכונה לחשוב ?״. שאלה זו היא מן הסתם אחת השאלות המאוחרות והפרובוקטיביות אשר נשאלו על מכונות. שכן, עד להמצאתם של המחשבים הספרתיים, תוכננו מכונות בעיקר כדי לבצע תפקידים מכאניים, ששאלת החשיבה או האינטליגנציה לא היתה רלבנטית להן, אף כי היו אנשים שנתנו דעתם עליה. אחד האנשים האלה היה הברון פון קמפלר, אשר המציא ב־1800 מכונה שמשחקת שחמט. ואמנם הצליחה מכונה זו לנצח את כל היריבים שהתמודדו עמה, ורק כעבור שנים התגלה שאת כושרה המופלא היתה חייבת מכונה זאת לשחמטאי אנושי שהסתתר בתוכה. הצד הפיקנטי במעשה נוכלות זה היה, שהצופים הורשו להציץ אל קרביה של המכונה, כדי לסלק מלבם כל ספק באשר לכשרותה, ואעפי״כ לא גילו דבר. כיום מצויות מספר תכניות־מחשב המשחקות שחמט ברמה של שחקני־תחרויות מתחילים. כלומר, מסוגלות לנצח את מרבית השחקנים החובבים. קיימת גם תכנית־מחשב המשחקת ״דמקה״ ברמה של שחקן בדרגת אמן. רוב האנשים מסכימים שמבצע כזה הוא הישג כלל לא מבוטל. השאלה היא אם אפשר לראות בו עדות לאינטליגנציה של המכונה, ועל כך נטוש הפולמוס. פולמוס הנובע יותר משיקולים רגשיים מאשר רציונליים.
מבחנו של טיורינג
שאלת חשיבתן של מכונות הועלתה על ידי הלוגיקן המפורסם א.מ. טיורינג1 בשנת 1950, ועד ימינו נחשבת האנליזה שלו לאחת המוצלחות ביותר מבחינת הבהרת הנושא.21 טיורינג היטיב לראות כי בעייתיותה של שאלה זו נובעת מהפירוש הסוביקטיבי שבני אדם מיחסים למושג ״חשיבה״.
רבים מאתנו יוצאים מנקודת הנחה מוקדמת שחשיבה היא תכונה אנושית, לפיכך מכונות אינן יכולות לחשוב (אלא אם כן ירצה מישהו לעורר את השאלה שמא מכונות הן אנשים, או שמא אנשים הם מכונות).
כדי להמנע משאלות מעורפלות הציע טיורינג מודל המאפשר לדון בשאלת המכונה ״החושבת״ במונחים טכניים גרידא. מודל זה קרוי ״המבחן של טיורינג״, והוא מבוצע כך: נתאר לעצמנו מחשב מ ואדם א, הנמצאים כל אחד בחדר נפרד וכל אחד מהם קשור באמצעות מסוף (מעין מכונת כתיבה המופעלת על ידי פולסים חשמליים המועברים אליה באמצעות כבל טלפוני — המערכת) לחדר שלישי, מקום בו מוצב הבוחן ב. תפקידו של ב לאתר איזה מסוף מחובר ל־מ ואיזה מסוף מחובר ל־א, וזאת באמצעות ניתוח התשובות של א ושל מ, המתקבלות דרך המסופים, לשאלות שהוא מעביר אליהם. מבחנו של המחשב מתבטא במידת הצלחתו להטעות את הבוחן, כך שלא יוכל להבחין על פי תשובותיו שהוא איננו אדם. מבחן זה הפך את השאלה הקודמת ״האם יכולה מכונה לחשוב״ לשאלה חדשה : ״האם יכולה המכונה לשחק את המשחק באופן מוצלח״. השאלה החדשה נראית פשוטה ולאין שעור פחות בעייתית מהשאלה הקודמת, אך גם כאן ניתן לשאול לכוונת המילים ״באופן מוצלח״. שהרי מוצלח או לא מוצלח הוא ענין של הערכה, אלא אם כן נקבע שקריטריון ההצלחה הוא סטטיסטי. כלומר, מה אחוז הסיכוי P שהבוחן ב יזהה את המכונה אחרי פרק זמן של ז דקות. הקוץ במבחנו של טיורינג מתגלה בבעיות התכנון ההנדסי ובמיוחד בבעיות של תוכנה שהוא מעלה, היינו; באיזו מידה נוכל לבנות מכונה שתשחק את המשחק באופן מוצלח. ייתכן שלא הכל יסכימו עם מבחן זה, אך הענין הרגשי שבשאלה המקורית שלנו נעלם ואיננו. במאמרו משנת 1950 מתנבא טיורינג, שלקראת סוף המאה כבר יהיו מכונות המסוגלות לשחק את המשחק בהצלחה, כך שלבוחן ממוצע לא יהיו יותר מ־70% סיכויי הצלחה לזהות את המחשב אחרי חקירה של 5 דקות.
לא ידוע לנו על קיומם של אנשים אשר ניסו הלכה למעשה את מבחנו של טיורינג. מאידך, עבודה רבה שהושקעה בנושא מאירה במידת־מה את השאלה : באיזה אופן לתכנת מחשב אשר יוכל להצליח במבחן טיורינג, ובאיזו מידה עשויה תוכנית כזו לעמוד בהצלחה במבחן לאור מצבו הנוכחי של התכנות ההאוריסטי.
כדי להצליח במבחן טיורינג, צריך המחשב לשוחח באופן סביר, באמצעות מלים מודפסות, באיזושהי שפה טבעית. קיימות מספר תכניות מחשב שמטרתן לנהל שיחה סבירה בתחום דיון מצומצם. נתאר להלן שתי תכניות כאלה, אשר נכתבו בשנים האחרונות, ונשאיר לקורא לשפוט בעצמו מה מידת הדיוק בתחזיתו של טיורינג.
תכניות שיחה.
תכנית המחקה באופן מוצלח בן שיחה טוב צריכה להיות מסוגלת לחקות היטב שתי תכונות אנושיות הבאות לביטוי בשיחתם של בני אדם. ראשית, היא צריכה להבין משפט או שאלה בכל אחת מהצורות הרבות אשר ניתן להציגם; כלומר, היא צריכה להבין את משמעותו של המשפט. שנית, היא צריכה לשוחח באופן סביר על נושא מסוים, אפילו אם אין העובדות הנמצאות ברשותה מאפשרות לה לתת תשובה בהירה. במלים אחרות, היא צריכה לתת תשובה סבירה על שאלות, כגון: ״מה אתה חושב על פיקאסו ?״.
ההבחנה בין ״הבנה״ לבין ״לענות באופן סביר״ היא לגמרי לא ברורה, אף שכל אחד מאתנו עמד בודאי בשני מצבים אלה פעמים רבות. היינו, לרוב אנו חותרים להבין את נושא דבריו של בן שיחנו, אך יש פעמים שאין לנו כל ענין בו ובשיחתו, ואז אנו רק מעמידים פנים כמקשיבים ומהמהמים תשובות לא מחיבות, כגון: ״כן״, ״מענין מאוד״ וכיו״ב.
אופינית היא העובדה, שכל תכניות השיחה שנכתבו עד היום מנסות להדגיש אחד משני אספקטים אלו, אך לא את שניהם. אנו נמצאים עדיין במצב שבו אנו מנסים לשכלל טכניקות בודדות במקום למזג מספר טכניקות בתכנית אחת. מבין התכניות שנכתבו בשנים האחרונות, שתי התכניות הקרויות ELIZA2 ו־ student מדגימות שני מצבים אלה (״שיחה עם מעט הבנה״ לעומת ״הבנה עם מעט שיחה״) באופן טוב למדי.
אליזה עצמה היא תכנית רב־תכליתית אשר מקבלת כקלט משפטים באנגלית ומרכיבה את תשובותיה מתוך משפטי הקלט, בהתאם למספר טרנספורמציות קבועות מראש הנקבעות על ידי ״תכתיב״ נתון.
אחד התכתיבים, הקרוי דוקטור, גורם לאליזה לשוחח עם אדם (באמצעות המסוף) בנוסח המזכיר מאוד תשובות של פסיכיאטר. הקטע הבא הוא דוגמא של שיחה שהתנהלה בין אליזה לאשה. תשובותיה של אליזה מודפסות באותיות גדולות :
כל האנשים דומים
באיזה מובן
הם תמיד מפשפשים בדבר זה או אחר
האם את יכולה לחשוב על דוגמא מסוימת
טוב, חבר שלי גרם לי לבוא לכאן
חבר שלך גרם לך לבוא לכאן
הוא אומר שאני מדוכאת רוב הזמן
אני מצטער לשמוע שהנך מדוכאת רוב הזמן
זה נכון, אני לא מאושרת
האם הנך חושבת שבואך לכאן יעזור לך לא להיות בלתי מאושרת
אני זקוקה לעזרה, זה ברור
מה זה אומר לך אם תקבלי עזרה
אולי אוכל ללמוד להסתדר עם אמי
ספרי לי עוד על משפחתך
אמי דואגת לי
מי עוד במשפחתך דואג לך
אבי
אביך
אתה דומה לאבי במובן מסוים
איזה דמיון את רואה
אינך מאוד תקיף, אבל אני חושבת שאינך רוצה שארגיש בכך
מה גורם לך לחשוב שאיני מ22אוד תקיף
אינך מתווכח אתי
מדוע את חושבת שאיני מתוכח אתך
אתה פוחד ממני
האם הנך מרוצה להאמין שאני פוחד ממך
אבי פוחד מכל אחד
מה עוד עולה במוחך כאשר את חושבת על אביך
נדנודים
האם יש לזה קשר לעובדה שחברך גרם לך לבוא לכאן
השיטה שמאפשרת לאליזה לתת תשובות כאלה מוסברת על ידי מתכננה, וויזנבאום (J. Weizenbaum) מ־MIT, כך: ״החלק העיקרי של התכנית הוא פשוט למדי: עם קריאת הטקסט מחפשת התכנית מילות מפתח. אם נמצאה מילה כזאת מופעלת טרנספורמציה הקשורה באותה מילת־מפתח, ואם לא נמצאה, היא פולטת הערה לא ענינית כלשהי המספקת לה משפט תגובה סתמי. ניקח, למשל, את המשפט: ׳אני מאוד לא מאושרת בימים אלה׳. אילו היה מושמע משפט זה באזניו של נוכרי, ששליטתו המוגבלת בשפה מאפשרת לו להבין מהמשפט רק את המילה ׳אני’, ואם הוא מעונין בהמשך השיחה (או שהוא מבקש להיות אדיב), יכול הוא להשיב במשפט הבא : ׳מדוע את לא מאושרת בימים אלה׳ ? לצורך זה עליו להיות מצויד במערכת הרכבה מתאימה, שתאפשר לו לתרגם כל משפט מסוג ׳אני״.׳ למשפט מסוג ׳מדוע אתה…׳, בלי שיצטרך להתיחס למשמעות המילים הבאות אחרי ׳אני׳. דוגמא מורכבת יותר היא המשפט : ׳כנראה אתה שונא אותי׳. כאן מבין הזר את המלים ׳אתה׳ ו’אותי׳ והוא מחלק את המשפט ל־4 חלקים, בהתאם לאחת התבניות הנתונות לו במערכת ההרכבה :
1) כנראה 2) אתה 3) שונא 4) אותי. מתוך ארבע מילים אלו הוא מבין רק את השניה והרביעית. אולם, בהתאם להוראותיה של מערכת ההרכבה, יכול הוא לענות, למשל; ׳מה גורם לך לחשוב שאני שונא אותך׳ ? כלומר, הוא יכול להתעלם מהמילה הראשונה, לתרגם את המילים המוכרות לו: ׳אתה׳ ל׳אני׳ ו׳אותי׳ ל־ ׳אותך’, ולהדביק,איזושהי קידומת, כגון: ׳מה גורם לך לחשוב ש־׳ בתחילת המשפט״.
התכתיב דוקטור מכיל בסה״כ כעמוד וחצי של הוראות הרכבה, ומפתיעה העובדה שמספר הוראות קטן יחסית זה יכול לייצר את השיחה שתיארנו. יתר על כן, אחת ממטרותיה של אליזה היא להסתיר את חוסר הבנתה. אי לכך, אם המשפט שהיא קולטת לא מפעיל שום כלל מן התכתיב, היא תשיב בנוסח מעין זה : ״בוא נדבר עכשיו על משהו אחר״, או; ״ספר לי על כך וכך״. תשובות כאלה אינן מחייבות להבין את הנאמר והן יפות לכל שיחה, בתנאי שאין הן נאמרות לעתים תכופות מדי.
התכנית השניה, סטודנט, אמורה לפתור בעיות אלגבריות המוצגות באופן מילולי, למשל: סכומם של שלושה מספרים הוא תשע. המספר השני גדול בשלוש מפעמיים המספר הראשון. המספר השלישי שווה לסכומם של שני המספרים הראשונים. מצא את שלושת המספרים.
עולמה של התכנית סטודנט מורכב מתאורים מילוליים של משוואות אלגבריות, במיוחד משוואות ליניאריות. כאשר מוצגים לסטודנט תאורים כאלה, מנסה התכנית לזהות את הנעלמים הקשורים בבעיה, את יחסי הגומלין שלהם ולתרגם את התאור המילולי למערכת של משוואות בצורה המתימטית המקובלת. בבעיה שהצגנו מזהה סטודנט את שלושת הנעלמים: f (ראשון), s (שני), t (שלישי), ואח״כ מציבה את מערכת המשוואות הבאה ;
f+s+t=9
s = 3 + 2f
t = f+s
הבעיה העיקרית היא להגיע לשלב זה שבו המשוואות כבר מוצבות. היתר הוא טריויאלי, שכן יש שיטות בדוקות לפתרון מערכת של משוואות ליניאריות. הנקודה המענינת היא כיצד מתרגמת סטודנט אוסף מילים
באנגלית למשוואות אלגבריות המובעות בצורה פורמלית. ניקח, למשל, שאלה זו: גילה של מרי הוא פעמיים הגיל של אן, כאשר מרי היתה בגיל של אן כיום. אם מרי היא בת 24 כיום, בת כמה אן ?סטודנט מסווגת את המילים והפסוקים של המשפטים לשלוש קטגוריות : משתנים, אופרטורים ומתמירים.
מתמירים הם פסוקים אשר סטודנט מציבה מיד במקום פסוקים אחרים. למשל, המלה ״פעמיים״ תשונה תמיד ל״כפול שתיים״. מטרתו של מתמיר כזה היא להפחית את מספר הצורות הלשוניות על ידי החלפת מספר רב של מבנים מיוחדים במספר קטן של מבנים כלליים. אופרטורים הם פסוקים המסמלים פעולות אריתמטיות אשר סטודנט מכירה (חבור, חסור, כפל, חילוק והעלאה בחזקה), או קומבינציות של פעולות אלה (כגון: ״הסכום של x ושל המכפלה של y ב־2״) וכן סימן השויון.
להלן מספר צורות לשוניות, אשר אפשר להשתמש בהן כדי להביע פעולות אריתמטיות ואת יחס השויון:
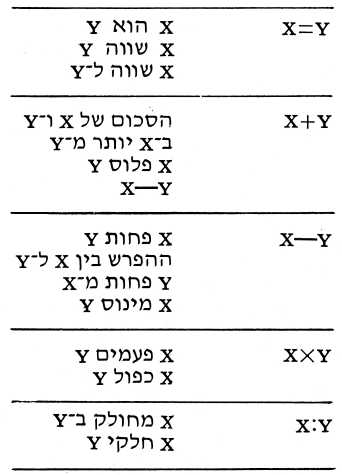
הקטגוריה השלישית של מילים ופסוקים המוכרים על ידי סטודנט היא קטגורית המשתנים. משתנה הוא סדרת מילים אשר נבחרת על ידי סטודנט כמייצגת של נעלם בבעיה שהיא צריכה לפתור. סטודנט אינה מנסה להבין את המשמעות של המשתנה ; כל מעייניה נתונים לזיהוי הפסוקים והמשתנים ואלו פסוקים מתיחסים לאותם המשתנים. אם סטודנט יכולה לפתור בעיה מילולית אשר בה מופיע המשתנה ״הגיל של אן״, היא יכולה לפתור בעיה דומה בה הוחלפה כל הופעה של ״הגיל של אן״ במלה חסרת משמעות כמו ״אבג״. העובדה שסטודנט אינה מנסה להבין דבר על אופי המשתנים מראה בבירור שיכולתה להכיר ולזהות פסוקים אשר מתארים אותם משתנים היא מוגבלת למדי. לדוגמא, סטודנט לא היתה מכירה בכך ש״הזמן שחלף מאז הולדתה של אן״ מתאר את המשתנה ״הגיל של אן״.
כעת נוכל לתאר את השיטה העיק23רית, שבעזרתה מכירה סטודנט משוואות אלגבריות הטמונות בביטויים מילוליים.
לאחר שכל המתמירים הוצבו, מחפשת סטודנט הופעות של אופרטורים, וזאת על ידי השוואת משפטי הקלט עם אותם אופרטורים המאוחסנים בקטלוג שלה. אח״כ היא מזהה את המילים שבין האופרטורים כמשתנים, ומחליטה אלו משפטים מסמלים אותם משתנים (כפי שנאמר לעיל, סטודנט תכיר ששני משפטים אכן מסמלים אותם משתנים רק אם הם זהים, או נבדלים במעט זה מזה).
אם משפטי הקלט נמנים עם הסוג שסטודנט יכולה להבין, אז בשלב זה תבנה התכנית סדרה של משוואות אלגבריות בסימון מתימטי פורמלי. אם היא יודעת כיצד לפתור משוואות אלה היא תמשיך בביצוע ותדפיס את התוצאה. אם לא, במקרים שבהם המשוואות אינן ליניאריות, או מספר המשוואות קטן ממספר הנעלמים, תשאל התכנית : ״האם יש קשרים נוספים בין המשתנים ?״. אם התשובה שלילית — תודפס ההודעה : ״איני יכולה לפתור בעיה זו״. מן הדין לציין שגישה זו מאפשרת לסטודנט לפעול באופן נאות למדי. מובן שלאחר שהבנו את אופן פעולתה, קל מאוד לבנות דוגמאות שיגרמו להכשלתה. למשל, בבעיה המכילה את המשתנה ״מספר הפעמים שראיתיה״ תזדרז סטודנט לזהות את המילה ״פעמים״ עם אופרטור הכפל, ואז תחשוב שמדובר בשני משתנים: ״מספר״ ו״שראיתיה״. למרות זאת, הבעיות שפתרה סטודנט מראות שבמסגרת האלגברית המצומצמת היא יכולה להתחרות בתלמיד תיכון ממוצע. עובדה זו נותנת משקל מסוים למסקנתו של D.G. Bobrow, אשר כתב את התכנית סטודנט: ״חושבני שאנו רחוקים מהאפשרות של כתיבת תכנית אשר יכולה להבין את השפה האנגלית במלואה, או אפילו מקטע נרחב שלה. אף על פי כן, במסגרת תחרותית צרה יותר הראתה סטודנט שניתן לבנות מכונות ׳מבינות׳ ״.
היכולה מכונה להכפיל את עצמה ?
תכונת ההכפלה העצמית, שהיא יכולתו של אורגניזם ליצור אורגניזמים בני דמותו, נחשבת לתכונה בלעדית של החיים ואף מסייעת זה תקופה ארוכה להבחין בין חי לדומם. ההישגים המעבדתיים האחרונים בקשר להכפלה עצמית של מולקולות מורכבות, הישגים אשר כונו בשם ״יצירת חיים במבחנה״, חזקו את ההבחנה המקובלת, שהכפלה עצמית וחיים הם מושגים שאינם ניתנים להפרדה. אבל העובדה שבכל זאת קיימות תופעות טבע אשר קשורות בעצמים דוממים, ואשר מזכירות מאוד את תכונת ההכפלה העצמית (למשל, גידולם של גבישים מינרליים), מורה על כך שמה שמבדיל חי מדומם אינו בהכרח כושר ההכפלה העצמית.
יש הטוענים, בדרגה לא מבוטלת של סבירות, כי מכונה אינה יכולה להכפיל את עצמה, וזה מהסיבות האלה: אם מכונה א׳ בונה מכונה ב׳, צריכה א׳ להכיל לא רק תאור מפורט של ב׳, כי אם גם מנגנונים המסוגלים לבקר את תהליך ההרכבה, כגון: מנגנון לפיענוח התאור של מכונה ב׳, זרועות מכניות וכיו״ב. פירוש הדבר שמכונה א׳ חייבת בכל מקרה להיות מורכבת יותר ממכונה ב׳. כלומר, מכונה מסוגלת עקרונית לבנות דגם פשוט יותר של עצמה, אך לעולם לא עותק מדויק של עצמה. הנסיון שרכשנו עם מכונות קיימות נראה כמאמת טיעון זה. מכונה אשר תפקידה היחידי הוא להדק ברגים, היא לעולם מורכבת יותר מהבורג עצמו. למרות שאינטואיטיבית נראה טעון זה נכון, הריהו מטעה. שכן, את האינטואיציה הזו רכשנו על סמך הנסיון שיש לנו עם מכונות פשוטות יחסית. אך היא אינה טובה כשדנים ביכולת פעולתן העקרונית של מכונות (במיוחד אם הן מורכבות). ג׳ון פון נוימן, שחקר ביסודיות בעיות אלו בשנות ה־50, התרכז בלימוד ״האוטומטים המכפילים עצמם״, הניתנים להגדרה ברורה, והניח לאורגניזמים אשר מורכבותם היא כה גדולה עד כי איש אינו מבינם ביסודיות.
פון נוימן הציע במחקריו מספר מודלים אשר שניים מהם נתאר. הראשון הוא מכשיר מכאני הבנוי באופן קונבנציונלי, כמכונה המורכבת ממספר חלקים אלמנטריים, ואילו השני הוא מודל אלגברי מופשט. למודל הראשון יש יתרון־מה בהיותו קשור אינטואיטיבית לנסיוננו עם מכשירים מכאניים, ולכן נוח יותר להמחיש באמצעותו את עקרונות בנייתה של המכונה־המכפילה־עצמה.
מאידך, חסרונה נעוץ בקושי שבבנייתה. המודל השני מנסה לעקוף קושי זה על ידי הצגת רעיון ההכפלה העצמית בצורה מופשטת, המאפשרת לגשת לתכנון מפורט של מכונה־המכפילה־עצמה. פון נוימן עצמו בחר בדרך השניה ותיאר את המודל על־פני מאתיים עמודים בערך. חסרונו של המודל השני נעוץ בקשיי הסברתו, לפיכך נקדים הסבר קצר על המודל.
במודל האלגברי, הקרוי לעתים קרובות ״מודל התאים״ או ״מודל המוזאיקה״, מוצג המרחב כמלבן אינסופי, דו־ממדי, המורכב מתאים ריבועיים זהים ; וכן מניחים שהזמן גדל ביחידות בדידות (…,0,1,2=T). כל תא יכול, עקרונית, להיות בזמן מסוים באחד מבין מספר סופי של מצבים. נניח, למשל, שהמצבים הם א, ב, ג, ו־ד. עם המעבר מזמן מסוים T, לזמן העוקב לו, 1+T, יכול כל תא לשנות את מצבו בהתאם לפונקציה נתונה מראש, הקרויה פונקציית המעבר. פונקציה זו קובעת מה יהיה מצבו של כל תא בזמן T+1, בהתאם למצבו הוא ובהתאם למצביהם של ארבעת התאים בשכנותו בזמן T, פרט כמובן למקרה שבו 0=T. בזמן 0=T (המצב ההתחלתי) אנו מניחים שכל התאים (פרט לקבוצה סופית) נמצאים במצב א, מצב שיקרא ״מצב אדיש״. תיתכן, למשל, פונקציית מעבר המורה להציב ב בכל התאים שהתא מימינם נמצא במצב האדיש ושלושת האחרים במצב א. ברור לנו מכך, שמשתופעל פונקציית מעבר זו נקבל מבנה ספציפי של מצבים הנובעים מהגדרת הפונקציה.
מה הקשר בין מודל התאים לבין המכונה־המכפילה־עצמה ? מסתבר שאנו יכולים להגדיר מבנה זה של תאים רצופים ומצביהם — בתוספת פונקציית המעבר — כ־ ״מכונה״. ״מכונה״ זו תיקרא מכונה־המכפילה־עצמה אם פונקציית המעבר שנפעיל על התאים תייצר בזמן סופי כלשהו מודל של תאים המאורגנים באותו מבנה ושמצביהם זהים לשלה, אך בתנאי שהזהות אינה נוצרת בעזרת תאים משותפים (ראה ציור).
עד כאן על המודל האלגברי. נחזור עתה למודל הראשון של המכונה־המכפילה־עצמה, המכשיר המכאני.
נדמה לעצמנו מחסן המכיל כמות בלתי מוגבלת למעשה של מספר סופי של חלקי מכונה. אלה יקראו ״החלקים האלמנטריים״, אשר מהם מורכבת המכונה־המכפילה־עצמה. אוסף זה של חלקים צריך להיות מגוון מספיק כדי לאפשר בנייתן של מכונות ניידות המונעות באופן עצ24מאי (למשל, גלגלים, הילוכים, מנופים, אומים, ברגים, סרטי נייר, מצברים וכו׳). תאור מדויק של אוסף זה של חלקים מהווה בעיה מסוימת, כפי שנראה להלן, אך לעת עתה נניח שאכן ניתן להגדירו באופן נאות. בעית המכונה־המכפילה־עצמה יכולה להיות מוצגת באופן הבא : האם עבור אוסף עשיר מספיק של חלקים אלמנטריים קיימת מכונה (המורכבת מחלקים אלה) אשר יכולה לטייל לה במחסן, לאסוף את החלקים הדרושים ולהרכיב מהם עותק של עצמה, וזו מצידה תוכל להמשיך ולהרכיב מכונה שלישית וכו׳ ?
נתרכז עתה בתאור אוסף החלקים. קל להתגבר על הקושי שבבעיה על ידי בחירה לא הגיונית של החלקים. ניקח מקרה קיצוני. נניח, למשל, שקיימת מכונה שיש לה היכולת להכפיל את עצמה, ונניח עוד שמכונה זו פועלת בעזרת מצבר (או רכיב פשוט אחר). נוכל, כמובן, לומר שהמכונה מורכבת משני חלקים : (א) כל המכונה פרט למצבר, (ב) המצבר עצמו. לפי הנחתנו, ברגע שיחובר המצבר תוכל המכונה להכפיל עצמה. לכן כל הבעיה כעת היא בעית חבור המצבר, ועל בעיה זו קל להתגבר. טיעון כזה משאיר אותנו בהרגשת־ מה של אי שביעות רצון, שכן איננו יודעים ממנו מה הן תכונותיו של חלק א׳ בזכותן יכולה המכונה להכפיל את עצמה. והלא יכולת זאת של הכפלה עצמית היא־היא התכונה שאנו מנסים לחקור.
מצד שני, אם נבחר חלקים מדי קטנים או מדי פשוטים, עלולות תכונותיה היסודיות של המכונה להתערפל מחמת ריבוי הפריטים המרכיבים אותה. אין כללים קשוחים להגדרת החלקים האלמנטריים. זה ענין לשכל הישר : הקריטריון לבחירה מתאימה של החלקים צריך להיות: האם הבעיה שמתקבלת היא ״מענינת״.
פון נוימן תאר בזמנו כתריסר קבוצות של חלקים אלמנטריים אשר בעזרתם ניתן, לדעתו, להרכיב מכונה, אבל הוא לא פירט איך לעשות זאת. במקום זאת הוא ״פירק״ את המכונה־המכפילה־עצמה לשלוש מכונות קטנות יותר, אשר אף אחת מהן לא היתה מסוגלת להכפיל את עצמה, ואשר כולן מכונות סבירות למדי. שלוש מכונות אלו הן (א) U — בונה אוניברסלי, (ב) D — מכפיל סרטים ו־(ג) C — אוטומט בקרה.
לא נתאר כאן את בנייתן המייגעת של מכונות אלו מחלקים אלמנטריים ; במקום זאת, נפנה לאינטואיציה של הקורא, ונאמר, שעקרונית ניתן לבנות אותן. לעומת זאת, נייחד את הדיבור על מכונות אלה עצמן ועל דרך פעולתן.
הבונה האוניברסלי, U, הוא החלק הקריטי במודל של המכונה־המכפילה־עצמה של פון נוימן. U היא מכונה אשר בהינתן לה התאור, (d(M, של מכונה כלשהי M, בונה העתק של M. האנלוגיה למחשב רב־תכליתי (אוניברסלי), אשר בהינתן לו זכרון מספיק גדול יכול לחשב כל פונקציה ״חישובית״, משכנעת את רוב האנשים הקרובים לנושא המחשבים — כי אכן מכונה כזאת ניתנת להבנות. מושג המכונה U הוא די קרוב לזה של קו־יצור בבית חרושת. תכנון מושלם של U (פרוט חלקיה, תאורה והאלגוריתם של בניתה) נראה כמאמץ הנדסי גדול, אבל בהחלט בתחום אפשרויותיה של הטכנולוגיה המודרנית. הבונה האוניברסלי U דורש לצורך פעולתו תאור חד־משמעי, בצורה ברת קריאה, של המכונה אשר אותה הוא צריך לבנות. דרישה זו מעוררת בעיה נוספת בבחירת אוסף החלקים האלמנטריים; כלומר, החלקים צריכים להיבחר כך שיבטיחו קיום של תאור סופי של כל מכונה M אשר יכולה להיבנות על ידם. תנאי זה אינו מהווה הגבלה של ממש, כיוון שסביר בהחלט לחשוב על אוסף של חלקים בעלי התכונה הבאה: אם שני חלקים ניתנים בכלל להתחבר זה לזה, אזי הם ניתנים להתחבר רק במספר סופי של אופנים. לאחר שנבחר אוסף מתאים של חלקים אין בעיה מיוחדת בתכנונה של שפה לתאור החלקים ולתאור האופנים בהם ניתן לחברם זה לזה. לצורך דיוננו נאמר, שתאור (d(M של מכונה M מקודד על פני סרט נייר, למרות שכל צורה ברת־קריאה אחרת אפשרית אף היא.
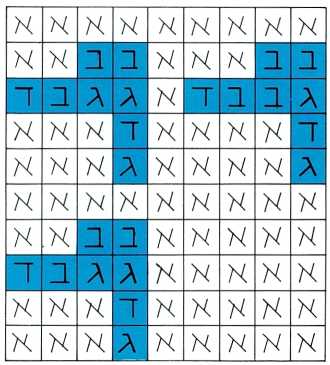
אחרי הפעלת פונקציית המעבר במספר סופי של פעמים, עשויים להתקבל במרחב המבנים הללו (הצורות המודגשות). המבנה העליון הוא ״המכונה״ המקורית. המבנה מימינו זהה לו מבחינת הצורה הגיאומטרית אבל שונה מבחינת מצבי התאים. המבנה התחתון מהווה עותק מדוייק של המבנה המקורי. לפיכך, אנו יכולים לומר שהמכונה אכן הכפילה את עצמה. (הציור מבוסס על מודל דומה שהופיע בסייאנטיפיק אמריקן).
שתי המכונות האחרות פשוטות הרבה יותר מ־U. מכפיל הסרטים, D, הוא פשוט מכונה אשר קוראת סרט נייר מנוקב ומעתיקה אותו על ידי ניקוב של סרט נייר ריק אחר — באותו מבנה כמו הסרט המקורי.
אוטומט הבקרה, C, הוא מכונה פשוטה אשר מבקרת את U בפעולתה על D. כלומר, מעבירה אותם ממצב אחד למשנהו, מכניסה סרטים לתוכם, וכו׳. תפקידה המיוחד של המכונה C יתבהר להלן, בעת תאור המכונה המורכבת U+D+C.
תהא M מכונה כלשהי ויהא (d(M התאור שלה — מנוקב על סרט נייר; ונניח ש־(d(M מחובר למכונה U+D+C. ראשית, מכניסה מכונת הבקרה C את הסרט (d(M לתוך מכפיל D, כך שיתקבלו עכשיו שני עותקים של (d(M. אח״כ מכניסה C עותק אחד של (d(M לתוך הבונה האוניברסלי U, אשר יבנה מכונה M בהתאם לתאור. לבסוף מחברת C את העותק השני של (d(M למכונה M החדשה, ומחברת שוב את העותק המקורי של (d(M למכונה U+D+C לכן, עבור מכונה כלשהיא M י (U+D+C+d(M בונה את (M+d(M. לכן, לצורך הכפלה עצמית, כל מה שנדרש הוא לחבר את הסרט (d(U+D+C למכונה U+D+C, ואז (U+D+C+d(U+D+C בונה בדיוק העתק של עצמה.
תאור זה מסיים את דיוננו במודלים של פון נוימן בדבר מכונות המכפילות את עצמן. ראינו מכונה אשר פועלת בסביבה מענינת (סביבה אשר חלקיה האלמטריים יכולים להיות כה פשוטים וידועים כמו אלה שאנו פוגשים בחיי יום־יום), בעוד שלמכונה עצמה יש התכונה הלא שגרתית של הכפלה עצמית, אשר לפי נסיוננו מתגלית רק ביצורים חיים. בכך זכתה השאלה שהצבנו בראש פרק זה למענה חיובי.
♦♦25





