התבוננו במפת האי הבריטי (איור 1). אם נמדוד את קו החוף מנקודה A ל-B בסרגל שיחידת המידה היסודית שלו היא מילימטר, ואחר כך נמדוד את אותו קו חוף בקטע המוגדל פי 2, נגלה להפתעתנו כי אורך קו החוף לא גדל פי 2 אלא ביותר מכך. ככל שנלך ונרד בקנה המידה (כלומר נגדיל את התצלום), כך יגדל אורך קו החוף שנקבל, והוא יגדל עוד יותר, אם נקטין את יחידת המדידה היסודית שלנו (ה״סרגל״), משום שנתחשב ביותר פרטים, כמו חצאי איים קטנים ומפרצונים. נשאלת השאלה, אם לקו החוף יש אורך ״אמיתי״, או שבכל פעם שאנו שואלים עליו, עלינו גם לשאול באיזה קנה מידה ובאיזה סרגל אנו מודדים. עניין זה תמוה וכמעט אבסורדי: ברור לנו כי גובהו של אדם או של הר לא ישתנו אם נשנה את קנה המידה או את הסרגל של מדידתם; מדוע אפוא ישתנה אורך קו החוף? אורך וגובה שניהם קווים, מדוע האורך משתנה בכל מדידה ואילו הגובה איננו משתנה?
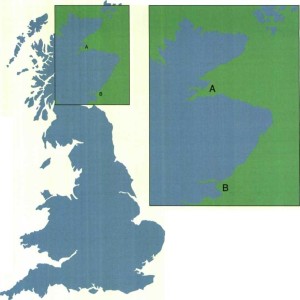

אם נשווה בין קווי החוף של ישראל (איור 2) לאלה של בריטניה (איור 1). נקל יהיה לראות, כי אורך קו החוף של בריטניה יהיה תלוי הרבה יותר בקנה המידה ובסרגל מאשר זה של ישראל, בגלל אופיו המפורץ יותר. כיצד נאפיין תכונה שונה זו של קו החוף של בריטניה? בנתון של אורך קו החוף בלבד אין כדי להמחיש את אופי החוף, כלומר עד כמה הוא מפורץ או חלק. נראה כי חסר כאן מושג – מושג הממד. מהו ממד בכלל וממד האורך בפרט, וכיצד יש להגדירו? בתחילת המאה הציע הוסדורף הגדרה פשוטה יחסית: אם נגדיל צלע של גוף במידה מסוימת, יגדל גודלו הכללי באותה המידה בחזקת הממד. מהגדרתו של הוסדורף יוצא, כי קווים הם בעלי ממד 1, משטחים הם בעלי ממד 2, וגופים בעלי נפח הם בעלי ממד 3.
הדוגמאות הבאות יבהירו זאת (קוראים הפוחדים ממתמטיקה יכולים לעבור לפסקה הבאה).
הממדיות הפרקטלית היא תכונה של מגוון רחב של תופעות וגופים טבעיים
עד כאן הכל נראה פשוט. אולם המתמטיקאים במאה הקודמת ובראשית המאה הנוכחית, וביניהם קנטור, קוך ופיאנו גילו מערכת כללים מתמטיים-גרפיים ליצירת גופים, שכאשר מחילים עליהם את ההגדרה המקובלת של הממד, ניתן לבטאו אך ורק באמצעות מספר שבור. העניין בצורות מתמטיות אלו לא חרג מעבר לגבולות של קהילת המתמטיקאים, ושם הן היו קרוב לוודאי נשארות. אולם ב-1975 הראה בגואה מנדלברוט ממרכז המחקר של יבמ ביורקטאון הייטס, כי הממדיות הפרקטלית אינה רק נחלתם של6 יצורים מתמטיים מופשטים, אלא תכונה של מגוון רחב של תופעות וגופים טבעיים. דוגמה אופיינית היא, כפי שראינו, קו החוף של ארצות ויבשות. אורך קו החוף הוא בעל ממד שבור, כי כאמור, הגדלת המפה פי x לא מגדילה את אורך קו החוף פי x אלא ביותר מכך. הסיבה היא, שקו החוף, כפי שהוא מצטייר במפה, מתארך ככל שקנה המידה שלה הולך וקטן, דהיינו ככל שמספר העיקולים והמפרצונים המתגלים בה הוא גדול יותר. מאותו הטעם עצמו, ככל שהחוף מפורץ יותר, כך גדל ממדו מעבר ל-1 (אך לא מגיע ל-2). על פי הגיון זה, ממד7 קו החוף של בריטניה גדול מזה של קו החוף הישראלי, כי הוא מפורץ יותר. כאמור, מנדלברוט לא המציא את המתמטיקה של היצורים המתמטיים הללו, (אם כי תרם את ״מפלצות מנדלברוט״ המפורסמות 1 ), אבל הוא היה הראשון שהראה, שתופעות רבות בטבע הדומם והחי מאופיינות על ידי ממדים המיוצגים על ידי מספרים שבורים – פרקטלים, כפי שקרא להם.

מנדלברוט היה הראשון שהראה, שתופעות רבות בטבע הדומם והחי מאופיינות על ידי ממדים פרקטלים
מעבר להבנת המוזרויות המתמטיות של התכונה הפרקטלית (שלא על כולן עמדנו), עשויה ההרחבה של מושג הממד לסייע לנו לאפיין נכונה תופעות רבות נוספות. לדוגמה, הכל מכירים את המסננים המורכבים על מסכות הגז שחולקו לנו במלחמת המפרץ. מסננים אלו מכילים חומר הקרוי פעיל שטח, בגלל שטח הפנים הגדול שלו ויכולתו לספוח גזים. את שטח הפנים של אבקות כגון פחם פעיל קובעים על פי כושרו לספוח גזים: מודדים את כמות הגז שנספחת (המייצגת את מספר המולקולות שנספחו), ומתוך ידיעת שטחה של כל מולקולת גז מחשבים את שטח הפנים של החומר הטופח. והנה מתברר, כי כאשר משתמשים בגזים שונים (מימן, בנזן, או גז חרדל) משתנה שטח הפנים של החומר הסופח. הסיבה לכך היא, שגז בעל מולקולות קטנות (מימן) ממלא את כל הנקבוביות והשקעים של החומר פעיל השטח, ואילו גז בעל מולקולות גדולות, כמו בנזן, “מדלג״ על חלק מהנקבוביות הקטנות, בדיוק כמו שיקרה, אם ננסה למדוד את אורך קו החוף בסרגלים שונים. יוצא כי גם כאן, בדומה לקו החוף, הגודל הנמדד (שטח הפנים) אינו ערך אובייקטיבי וקבוע. אנו רואים אם כן, כי אין להתייחס לגוף טבעי כאל משטח או נפח בלבד. בהתאם להשקפה המסורתית, כל שטח, ולכן גם שטח הפנים של הפחם הפעיל שבמסנן9 מסכות הגז, הוא בעל ממד 2, אולם במושגים פרקטליים הוא בעל ממד של כ-2.7 דהיינו, למרות ״דו ממדיותו״ הוא אינו שטח חלק בדומה לכדור פינג פונג, אלא דבר מה נפחי, הקרוב יותר לגוף תלת ממדי.
דמיון עצמי
לגופים פרקטליים יש תכונה נוספת חשובה מאוד, תכונת הדמיון העצמי. למה הכוונה? נניח שאדם מטייל בשדה ומבחין במרחק רב ממנו בבתים של מושב. מאחר שהוא יודע שגובה בתי המושב הוא בין שלושה לארבעה מטרים, הוא מסוגל לאמוד את המרחק שלו מן המושב על פי גודל הבתים. אולם מה היה קורה, לו היה המטייל שלנו מתקדם כדי מחצית המרחק, ואף על פי כן הבית לא היה גדל לעיניו פי שניים, אלא נשאר באותו גודל? יש להניח שהוא היה מאבד לחלוטין את תחושת המרחק.
ואכן, זה מה שקורה לטייסים הטסים מעל הים. מגובה רב הם מבחינים רק בגלים הגדולים, והם מתרגמים גודל זה למרחק שלהם מפני הים. הבעיה היא, שכאשר הם מנמיכים לטוס, מתגלים לעיניהם הגלים הקטנים יותר, שלא הבחינו בהם קודם, הנראים בדיוק כמו הגלים הגדולים. הדבר גורם לכך שתחושת הגובה – קרי המרחק מפני הים – משתבשת אצלם. בגלל תופעה זו של דמיון עצמי עלולה טיסה נמוכה מעל הים או מעל דיונות חול להיות מסוכנת. ובכן, ההבדל בין המטייל לטייס נעוץ בכך, שבמקרה הראשון הבית הוא גוף ארכיטקטוני יחיד, משולל כל מבנים הדומים לעצמם, ועל כן גודלו וצורתו משתנים מזוויות שונות וממרחקים שונים; לעומת זאת, מכל מרחק ומכל זווית שהטייס מסתכל על הים, הוא רואה אותם דגמים של גלים, ולפיכך אינו יכול להיעזר בהם כדי לאמוד את מרחקו מפני הים. זוהי תופעת הדמיון העצמי, והיא תכונה יסודית ובסיסית לא רק של גלים ודיונות חול, כי אם של כל הגופים הפרקטליים, כגון קווי חוף, עננים, תצורות של ברקים, רשת כלי הדם בגוף וגלקסיות סליליות.

אם הטבע הוא פרקטלי וממדי העצמים שלו שבורים, כיצד נוצרו הנקודות, הקווים, המשטחים ושאר הגופים הגיאומטריים בעלי הממד השלם? התשובה היא, שהגיאומטריה היא יציר רוחו של האדם. יצרו אותה המצרים הקדמונים כטכניקה לחלוקת שדות לשם השקייתם במי הנילוס. היוונים הקדמונים הפכו את הגיאומטריה למדע והשתמשו בה גם לצרכים אחרים, כמו אסטרונומיה וארכיטקטורה. אפלטון ואריסטו היו חלוקים בדעתם על משמעותם האונטולוגית של מושגי הגיאומטריה, כלומר בשאלה אם הם באמת ״קיימים״ בעולם ואיזה ״סוג״ של קיום אפשר לייחס להם – מחלוקת שלא הוכרעה עד היום. עתה, אחרי שהטבע גילה לנו את אופיו הפרקטלי, נראה שיש להתייחס לקווים, למשולשים ולשאר הגופים הגיאומטריים בעלי הממדים השלמים כאל הפשטות של המציאות, שנועדו לצרכים הנדסיים ושימושיים של היום יום. מה שמבחין בין שני סוגי העצמים – ה״רגילים” בעלי הממד השלם, והפרקטליים בעלי הממד השבור – הוא השתייכותם השונה: בסוג הראשון נמצא בעיקר עצמים מלאכותיים מעשה ידי אדם כמו בניינים, שולחנות, כיסאות ושדות תעופה, שלכולם סדרי גודל קבועים, כיוון שתוכננו לשמש את האדם והם מותאמים למידותיו ולצרכיו, ואילו בסוג השני נמצאו בעיקר תופעות ועצמים טבעיים. אפשר לומר, שכשם שהחדירה לעולם התת אטומי פתחה לפנינו את הדלת לעקרון האי ודאות – ובאמצעותו להבנה עמוקה יותר של הטבע, כך מביאה עימה הבנת הפרקטליות של הטבע ממד חדש של הבנת הטבע.
פרקטלים וכאוס
בדרך כלל, כאשר מדברים על פרקטלים, קושרים אותם לתורת הכאוס. מה בין תורת הכאוס לבין פרקטלים? תורת הכאוס החלה להתפתח באמצע שנות ה-60, ופרצה לתודעת הציבור בתחילת שנות ה-80, עם צאת ספרו של ג׳יימס גליק ״כאוס״2. יש גורסים, כי תורה זו מביאה לסופה את תקוותם של המדענים לתיאור דטרמיניסטי, ולו סטטיסטי, של עולמנו, תיאור שיתבסס על חוקי טבע המנוסחים על ידי משוואות מתמטיות, שניתן לפותרן בהינתן תנאי ההתחלה. תקווה זו התחילה לשגשג עם הצלחתה העצומה של הפיסיקה הניוטונית, שהסבירה באמצעות מספר מצומצם של חוקים פשוטים הן את התנועות על פני כדור הארץ והן את תנועות גרמי השמים. לעומת זאת, תורת הכאוס מצביעה על מערכות ששוררים בהן משובים בלתי לינאריים (דהיינו מערכות משוב שבהן התגובה לגירוי איננה נמצאת ביחס ישר לעוצמת הגירוי). בחלק מהמערכות האלה, גם אם נכיר את המשוואות המתארות אותן, לא נוכל לחזות במדויק את מצבן העתידי. לדוגמה, אם נפתח ברז ונגיע למצב של זרימת מים אחידה, נוכל לחשב במדויק את כמות המים הזורמת בכל פרק זמן נתון. זוהי מערכת לינארית שתוצאותיה – קרי מצביה העתידיים – ניתנים לחיזוי. כעת, אם נפתח את הברז קצת יותר או נסגור אותו כמעט עד הסוף, הזרימה כבר לא תהיה אחידה, ולא נוכל לחשב את כמות המים המדויקת שזרמה מן הברז בכל יחידת זמן נתונה. זוהי מערכת כאוטית. מערכות כאוטיות הן כאלה, שבהן אין שני מצבים זהים, ולמשוואותיהן אין שני פת10רונות זהים, וגם אין דפוס מחזורי של תוצאות, החוזר על עצמו.
מערכות כאוטיות הן כאלה שבהן אין שני מצבים זהים
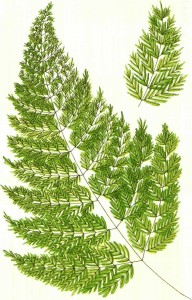

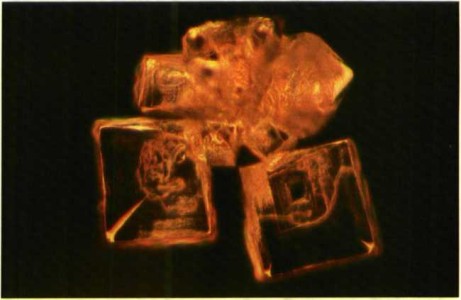
מתברר שתופעות רבות בטבע הן כאוטיות, והמשמעות היא שהטבע אינו ניתן לחיזוי לא רק בעולם המיקרוסקופי, אלא גם בעולם המאקרוסקופי הגלוי לעין – בניגוד מוחלט להשקפה הניוטונית והאינשטיינית. אם זהו המצב, איך זה שאנו חוזים בדרגת דיוק זו או אחרת את התוצאות העתידיות של מערכות ותהליכים טבעיים כאוטיים? ההסבר הוא, שאמנם אין לנו אפשרות לקבוע במדויק את המצבים העתידיים – התוצאות – של המערכות הללו, אך ברמת המאקרו הן יוצרות דגמים מוגדרים, לכן החיזוי הוא בכל זאת אפשרי. נסתכל למשל במבנה השרך (איור 6). אילו היינו אמורים לנבא באיזה מקום בדיוק יתפצל ענף מן ה״גזע״, לא היינו יכולים לעשות זאת בוודאות, וכך גם לו היינו אמורים לנבא בדיוק באיזו נקודה על הענף יגדל העלה ובאיזה מקום בדיוק על העלה יצמח לו עלעל קטן כלשהו. אבל היינו יכולים לנבא בוודאות גדולה, שיתקבל מבנה אופייני של שרך ולא של שיח שושנים, למשל. כלומר, ניתן להראות כי כל התוצאות, זאת אומרת כל מצבי המערכת העתידיים, ״נופלות” לתוך תחום, היוצר דגם שצורתו ניתנת לחיזוי, ואין פיזור או בריחה של התוצאות לאינסוף. האי ודאות היא לפיכך בגבולות מוגדרים. והנה מתברר, שכאשר מציגים מערכות ותהליכים כאוטיים כאלה באופן גרפי, הם מתווים מבנים פרקטליים מובהקים. כך למשל, בתנאים טבעיים11 ולא מבוקרים (״כאוטיים״) של גיבוש מלחים, מתקבלים גבישים פרקטליים ולא הגבישים הרגילים ה״חלקים” בעלי הממד השלם, המתקבלים בתהליכי גיבוש לינאריים מבוקרים (איור 7).
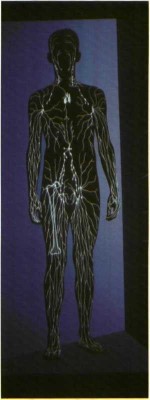
תופעה פרקטלית מעניינת במיוחד היא התפלגות כלי הדם בגוף. מערכת כלי הדם צריכה לעמוד בכמה דרישות כדי למלא את תפקידיה כספקית חומר ואנרגיה וכמפנה פסולת מכל הרקמות והתאים בגוף. דרישה אחת היא נוכחות של שני כלי דם ליד כל תא; דרישה אחרת – עליהם להיות גדולים דיים כדי לנקז כל זאת ל״פילטר״ אחד ול״משאבה״ אחת, אבל עליהם גם לקטון בכמה וכמה סדרי גודל ולהפוך לזעירים ביותר כדי לטפל בתאים יחידים. לכאורה, כמות המידע הגנטי לתיכנון ארכיטקטורה מורכבת ומדויקת כל כך צריכה להיות עצומה, אולם תורת הכאוס והפרקטלים עשויה להציע פתרון פשוט, שידרוש כמות מידע גנטי מינימלי. פתרון זה יהיה מבוסס על מנגנוני יצירה כאוטיים בלתי לינאריים, כמו אלה של ״מפלצות מנדלברוט”, היוצרים צורות פרקטליות מסובכות אך בעלות דמיון עצמי בכל קנה מידה, והמסתעפות מעצמן כתוצאה מחוק אחד, מנוסחה אחת, שיכול להיות פשוט מאוד. אמנם עדיין לא התגלה קשר כזה בין מידע גנטי, מנגנון ביוכימי ומהות מורפולוגית, אולם תיאורטית האפשרות קיימת, ואם הדבר יתגלה, יהיה בו כדי לשפוך אור על מנגנוני הקידוד הגנטי.
מאז גילה מנדלברוט את האופי הפרקטלי של הטבע, זוהו תופעות טבע כאוטיות רבות, שיאה להן התיאור הפרקטלי. רעשי אדמה, שטרם נמצאה שיטה לחיזוים, התפלגות של נפט בעורקים תת קרקעיים, צורותיהם של עננים, קווי חוף, ואפילו תנודות המחירים בבורסות. עוד12 אספקט קושר את תורת הכאוס והפרקטלים, והוא מה שקרוי ה״מושך״. מושך הוא במקורו מושג מתמטי, המציג תכונה של פונקציות מסוימות. ישנן פונקציות אשר אם נציגן באופן גרפי, נראה הרבה נקודות (שהן פתרונות של הפונקציה), אבל נראה אזור שבו ישנה צפיפות גדולה במיוחד של נקודות, וזהו המושך של הפונקציה. דוגמה פשוטה יכולה להבהיר זאת. הסתכלו בתמונת הגלקסיה (איור 8). לכאורה, פיזור הכוכבים בגלקסיה הוא אקראי וכאוטי. אולם אם נתעמק במראה, נראה שבאזור מסוים צפיפות הכוכבים גבוהה בהרבה מאשר בחלקים האחרים של הגלקסיה. אפשר לומר כי אזור זה הוא המושך של הגלקסיה. הדבר אופייני לחלק מהמערכות הכאוטיות, שבהן כאמור אין שני מצבים – שני פתרונות – זהים, אבל יש אזור מסוים (או אזורים מסוימים), שבו תדירות הפתרונות גבוהה יותר. כלומר, בהצגה גרפית של הפתרונות נקבל באזור מסוים צפיפות גדולה של נקודות (פתרונות). אזורים כאלה הם המושכים של המערכת. גם מערכות כאלה הן בעלות מבנים פרקטליים המאופיינים בדמיון עצמי גבוה, וככל שנתבונן במושכים הללו ביתר פירוט, כך נשוב ונראה אותה תמונה בקני מידה הולכים וקטנים.

איור 8: בגלקסיה נבחין באזור בעל צפיפות כוכבים גבוהה במיוחד. אפשר לומר כי זהו המושך של הגלקסיה.
הזמן הפרקטלי
הגדרת הממד קשורה גם בתפיסתנו את החלל וגם בתפיסתנו את הזמן, הקשור בתפיסת החלל. רובנו, גם אלו מאיתנו המכירים את תורת היחסות של אינשטיין, חושבים במונחים ניוטוניים של ה״חלל המוחלט״ ושל ה״זמן המוחלט”, זמן ה״זורם״ בקצב אחיד וקבוע. גישה זו נוחה ושימושית בחיי היום יום, אולם בעולם הטבע הפרקטלי מתערערת תחושת החלל המוחלט, והיא עלולה להטעות. עלינו אפוא לשוב ולבחון את מושגי החלל והזמן שלנו, ואולי ניאלץ להשתחרר מאופני החשיבה האינטואיטיביים האויקלידיים-ניוטוניים שבהם אנו שבויים, ולאו דווקא מנימוקים הקשורים בתורת היחסות.
לתופעות טבע כאוטיות רבות, יאה התיאור הפרקטלי
מושג הזמן שהורגלנו אליו באופן אינטואיטיבי נובע ככל הנראה משני מקורות. הראשון מקורו טבעי, והוא מתבסס על תנועות מחזוריות של כדור הארץ. השנה מתבססת על סיבוב כדור הארץ סביב השמש, והיממה – על סיבוב כדור הארץ סביב צירו. השעונים הטבעיים הללו מחלקים את תקופת חיי האדם לכמה עשורי שנים, ואת השנה ל-365 (ליתר דיוק 365.25) יממות. יחידות קטנות מיממה,13 שעות, ניתנות לנו על ידי השינוי המדומה במיקום השמש ברקיע במשך היום, והכוכבים בלילה. האדם גם המציא שעונים מלאכותיים, המחלקים את יחידות הזמן הטבעיות לחלוקות משנה על ידי תנודות קבועות: תנודות אטומיות (שעונים אטומיים), תנודות אלקטרוניות (שעונים דיגיטליים), תנודות מכניות (מטוטלות) ותנועה סיבובית קבועה (שעונים אנלוגיים). השעונים המלאכותיים מנסים לחקות את הטבעיים על ידי אילוץ מערכות להתנדנד באופן מחזורי קבוע, למשל על ידי מטוטלת, שקפיץ מחזיר לה את האנרגיה שהיא מאבדת. תפקידם של השעונים מסתכם בחלוקה פנימית של הזמן, שאין בה משום הגדרה של סטנדרד יסודי, אמת מידה בסיסית של הזמן, כפי שקיים סטנדרד של משקל או של אורך. לכן אין השעונים מלמדים אותנו דבר באשר למהות הזמן ולאופן שבו הוא נקבע בתודעתנו. כיצד אנו קולטים את המושגים הפיסיקליים הבסיסים? ז׳אן פיאז׳ה הראה, שמושג הזמן מתפתח אצלנו בשלבי הילדות ומקבל עיצוב סופי בשלב לימודי הפיסיקה בבית הספר התיכון ובמסגרת עולם מושגים זה.
בפרק זמן זה אנו מפנימים את הנוסחה הבסיסית, שאותה לומדים תלמידי התיכון בראשית התוודעותם לפיסיקה, האומרת ש״המהירות היא המרחק חלקי הזמן״. בכך אנו מקבלים ללא עירעור הן את המרחק כמושג יסודי וראשוני (שאינו מצריך הגדרה או הסבר נוסף) והן את הזמן ככזה, ובאמצעות שניהם מגדירים את מושג המהירות.
בבואנו להגדיר מושג אחד באמצעות שניים אחרים במערכת של שלושה מושגים, עלינו להחליט מהם שני המושגים היסודיים מתוך השלושה, שעליהם אנו מתבססים. היום, לאחר פיתוח תורת היחסות, שבה נקבעה מהירות האור כגודל יסודי מוחלט, ברור שיש להתבסס דווקא על המהירות – מהירות האור – כגודל יסודי וראשוני, כיוון שהוא אינו תלוי בצופה, במערכת הייחוס, באמצעי המדידה או במהירות המקור. עובדה זו ״משחררת״ את אחד משני המושגים האחרים, הזמן או המרחק, מהיותו יסודי, ראשוני או מוחלט. ואכן, באסטרונומיה מגדירים את המרחק באמצעות הזמן שעובר האור (שנות אור). אולם אפשר גם להפוך את היוצרות ולהגדיר את הזמן באמצעות מהירות האור ומרחק. היפוך יוצרות כזה נראה מוזר ממבט ראשון עקב קיום השעונים הטבעיים, הנותנים לנו תחושת זמן אינטואיטיבית חזקה. אולם אינטואיציה זו היא מקרית. אפשר להעלות על הדעת מצב שבו היה כדור הארץ תלוי בחלל מול השמש ללא תנועה סיבובית, למשל על ידי איזון גרוויטציוני מול שמש נוספת, או שהתנועה של כדור הארץ סביב שתי השמשות היתה מורכבת ומסובכת (ואפשרויות כאלה אינן בדיוניות לחלוטין, משום שהתגלו ביקום מערכות של ״כוכבים כפולים״). במקרים כאלה לא היתה יכולה להתפתח אינטואיציה חזקה של זמן. כיצד היינו מגדירים אז את הזמן? נראה שלא היתה ברירה אלא להסתמך, תיאורטית, על מהירות בסיסית כמו מהירות האור ועל מדידת מרחק, ובעזרתם לפתח את מושג הזמן. זהו זמן שאיננו עוד אינטואיטיבי וטבעי.

עתה, עם ההכרה הפרקטלית של הטבע ועם ההבנה שבטבע אין מרחק מוחלט, דבק גם בזמן, המוגדר על ידי המרחק, שמץ מהאופי הפרקטלי, והוא חדל ״לזרום״ בקצב אחיד וקבוע גם ללא הזדקקות ל״שמש נוספת״ וגם לא משיקולי תורת14 היחסות. נראה כי המדע שוב מרחיק את האדם מתמונת עולם מסודרת ופשוטה. העולם של ניוטון ולאפלאס הולך ונמוג לתוך ערפילים פרקטליים עמומים וסובייקטיביים, התלוים בצופה ובקנה המידה היחסי שבחר, דבר המזכיר את אחת המסקנות של פיסיקת הקוואנטים, זו שלפיה לצופה ולמכשיר המדידה שהוא בוחר יש משקל מכריע בתמונת העולם המתקבלת. העולם ה״מדעי״ המסודר, הדטרמיניסטי והאובייקטיבי ספג מידי מנדלברוט וממשיכי דרכו את המכה השלישית אחרי תורת היחסות הפרטית והכללית של אינשטיין ואחרי פיסיקת הקוואנטים של פלנק, בוהר, שרדינגר, הייזנברג, דה-ברוי ודירק, שגילו את חוסר הוודאות והדו משמעות הטבועים בטבע. מנדלברוט ועמיתיו חשפו בפנינו עולם כאוטי של דברים ״בינוניים״, יומיומיים (לא גדולים מאוד או מהירים מאוד כמו בתורת היחסות, ולא קטנים מאוד – כמו בפיסיקת הקוואנטים). זהו עולם של משובים בלתי לינאריים, הנאבקים ביניהם. על עולם כזה יש גם להחיל לוגיקה חדשה, כמו למשל הלוגיקה העמומה של זאדה Zadeh 3 . ואכן, לוגיקה עמומה זו מתחרה בהצלחה ביישומיה הטכנולוגיים עם לוגיקות “ודאיות״ יותר. נחשף אפוא בפנינו עולם חדש ומוזר, קסום לא פחות מהעולם הישן, שהיה לכאורה מסודר ופשוט.

הפרקטלים המוסיקליים של מהלר
רבים טוענים, כי יש קשרי גומלין בין התפתחות המדע ובין הרקע התרבותי והחברתי שבו הוא מתפתח. המהפכה של קופרניקוס, גליליאו וניוטון היתה חלק משמעותי מהוויית הזמן החדש, שבו שאף האדם להשתחרר מכבלים מעיקים של תורות ודוגמות נוקשות בכל תחומי החיים ולבסס עולם רציונלי. האם נכון יהיה לומר, שהתרחשות דומה והשפעות גומלין כאלה חלו במאה שלנו, מאה שרבו בה התהיות והספקות, והתקווה לתמונת עולם דטרמיניסטית התערערה עקב תורת הקוואנטים, תורת היחסות, ועתה רכבת, מעלית או מכונת כביסה. ההצלחה הטכנית של מערכות אלו מפתיעה. ביתר שאת עקב תורת הכאוס, שהכניסה את האי ודאות לעולם הדברים הבינוניים ולקני מידה אנושיים ״רגילים״. אמנם ייתכן, ואין לשלול על הסף אפשרות כי האי ודאות הקוואנטית של העולם התת אטומי מחלחלת אף לעולם של קנה המידה הבינוני, שעליו חלה תורת הכאוס, אולם מנגנון כזה טרם התגלה. מכל מה שנאמר עד כה, לא יהיה זה מוזר להניח, שהתוכנות החדשות יתבטאו בתחומים נוספים, למשל בתחומי האמנות. אתן לכך דוגמאות אחדות.
עם ההכרה הפרקטלית של הטבע דבק גם בזמן שמץ מהאופי הפרקטלי
תמונת הזמן הפרקטלי, העשוי להתכווץ או להימתח, בוודאי עוררה אצל הקורא15 אסוציאציה לתמונתו המפורסמת של סלוודור דאלי, תמונת השעונים הנוזלים, שמחוגיהם מתמסמסים וספרותיהם הולכות ונעלמות.
דוגמה מובהקת להמחשת הזמן הפרקטלי קיימת במוסיקה של מהלר
הזמן עומד ביסוד המוסיקה, אמנות המתבטאת במישור הזמן בלבד. פעמים רבות תהיתי, מדוע מוסיקה קצבית מעוררת ומושכת את בני הנעורים, מה יש בו בקצב, שהוא ״מדליק” כל כך. הרי אין זה סיפוק צרכים בסיסיים כמו מזון או מין. לא יכולתי להימנע מהמחשבה, שהקצב נותן למאזין תחושת זמן חזקה ביותר. המאזין ״חש״ ומרגיש את יחידות הזמן לא כזמן ש״נמרח״ בטווח של דקות ארוכות, אלא מתבטא בכל שנייה, בכל פעמה, בכל ביט, שהם בעלי משמעות וקיום לעצמם. זוהי תחושת הקצב, והסיפוק המיידי שקצב זה נותן למאזין 4 . נראה שלאדם יש צורך לא רק באוכל ובמין, אלא גם בתחושת זמן חזקה. העובדה, שרבים מוכנים לשלם תמורת זאת במיטב כספם ושמוסיקת הפופ היא צורת הביטוי האמנותית הנצרכת ביותר, מאששת השערה זו.

למוסיקה בכלל ולמלודיה בפרט יש משמעות נוספת. המלודיה היא קו בעל התחלה, אמצע וסוף, המתמשך בממד הזמן, והיא נותנת סיפוק למאזין בכך שהיא ממחישה ממד זה ויוצקת בו תוכן. זהו אולי ההסבר לתחושת הסיפוק בהאזנה לנושא שהולך ומתפתח, ובמיוחד לאילתורי ג׳ז משובחים. וכשהזמן גם הוא פרקטלי, יש לחפש לו ביטוי באמנות הממחישה אותו – במוסיקה. דוגמה מובהקת להמחשת הזמן הפרקטלי אני מוצא במוסיקה של מהלר, אשר עוררה השראה גם אצל מיצ׳ל פייגנגאום, מאבות תורת הכאוס. אם נאזין לסימפוניות של מהלר, בייחוד לראשונה ולרביעית, ובעיקר לפרק השלישי בסימפוניה הראשונה, המבוסס על הנעימה העממית המוכרת ״אחינו יעקב״ (פררה ז׳ק), נחוש תחושה מוזרה של קווים מלודיים המסתיימים לפני שפותחו, צלילי נושאים המופיעים כרמז הרבה לפני הופעתם המלאה (והמוכרים כמובן למי שכבר מכיר את היצירה), נושאים המתפתחים מצלילי נזשאים אחרים, נוטלים את שרביט ההובלה ושוב נמוגים, שזורים זה בזה, נובעים האחד מן השני ומן השלישי, ומכסים ומאפילים זה על זה. זוהי המחשה של תבנית זמן פרקטלית. התפתחות הנושאים יוצרת במאזין תחושת זמן ההולכת ונמוגה, ושבה ומופיעה בפסוקים בעלי אורך משתנה. הנושאים כה שזורים זה בזה, עד כי המאזין יכול לדלג בכל רגע מנושא לנושא, ולפיכך לבנות לעצמו את היצירה בכל פעם באופן שונה ובדינמיקה אחרת. ההתפתחות המלודית מבטאת וממחישה את תבנית הזמן הפרקטלית, שהיא שונה אצל כל מאזין ומאזין, ואף אצל אותו מאזין בהאזנות חוזרות. וכשאתה מכיר את היצירה ומנסה למצוא נקודת זמן שבה מופיע נושא שלם במלוא הדרו, כדי שתוכל לזהות מעין תזכורות ממנו בקטעים אחרים (כפי שנושאים מוכרים ואהובים מופיעים בסימפוניות של בטהובן) – לא תמצאם אצל מהלר. אתה נתקל רק בשברים, ברסיסים וברמזים, אשר באים,16 נקטעים ונמוגים. את השלם אתה מרכיב בדמיונך מתוך ראיית כל הרסיסים לאורך ציר הזמן. אבל הזמן, שהומחש על ידי זרימת הנושא בסימפוניות הקלסיות, נשבר כאן לזרמים ולתת זרמים בעלי מקצב וגוון שונה. השלם ניכר רק לפי פרודותיו, אך הפרודות אינן שברים מרוסקים של השלם, אלא מרכיביו החיונים בקני מידה שונים של זמן. הדבר בולט בהופעת נושאי הסיום בפרק האחרון של הסימפוניה הראשונה פעמיים, כך שתחושתך ״נמצאת״ בסיום הרבה לפני הגיעו כרונולוגית. גם צלילי הסיום עצמם, המופיעים בתרועת חצוצרות וטרומבונים חגיגיים, נקטעים בשתי פעמות חפוזות. אלו רק מעט מהדוגמאות המצויות ביצירה מופלאה זו, המדגימות את תחושתי. האם היה מהלר המהפכן בתחומו, מבשר העולם הפרקטלי במישור הזמן או מנסחו הראשון? ייתכן. אף ייתכן שבמקביל לו פעלו מבשרים של העולם הפרקטלי בתחומי אמנות אחרים, כפיקאסו, למשל, שהחלקים המרכיבים תמונות מסוימות שלו מופיעים בצורה כאוטית, ללא קשר “טבעי״, בקצב ובמקום לא צפויים, גישה שהדהימה את העולם עם הופעתה. ניסיתי להציג השקפה, שלפיה הזמן כגודל פיסיקלי בסיסי, העוזר לאדם לארגן לעצמו את עולמו בצורה נוחה, אינו אלא יציר רוחו של האדם, בדומה למושגים הפיסיקליים והגיאומטריים המקובלים האחרים, ואינו מושג ״בסיסי”, הטבוע באמת בטבע. הפיסיקאים מתלבטים באשר לאיפיון מושג הזמן גם מבחינות אחרות, כמו הסימטריה או חוסר הסימטריה שלו בטבע ובחוקי התרמודינמיקה, ולא נגעתי בזה כאן. ניסיתי להוסיף לנושא המרתק עוד זווית ראייה, גם אם היא הוסיפה אי ודאות, עירפול ועמימות פרקטלית. ■

“מפלצות מנדלברוט״ הן תוצרי הליך מתמטי של חישוב חוזר (איטרציה) של פונקציה של שני משתנים, המבטאים נקודות ציון על צג המחשב, כאשר תוצאה (פלט) של שלב חישוב אחד מהווה נתון (קלט) לשלב הבא, וכן הלאה. ↩
ספרית מעריב, תרגום: עמנואל לוטם ↩
ה״לוגיקה העמומה” (fuzzy logic) היא שיטת בקרה טכנית, שאת היסודות המתמטיים שלה הניח זאדה, ופיתוחיה הטכניים מיושמים היום בעיקר בתעשייה היפנית. במסגרת לוגיקה זו מגדירים מצב של מערכת כפי שאדם מגדיר גדלים באופן אינטואיטיבי, כגון: “מהר מאוד”, “קצת מקריח”, “גובה בינוני” ו״כבד למדי”. מזינים הגדרות עמומות אלו למערכת בקרה, היא משקללת אותן, ונותנת הנחיות למערכת שעליה היא שולטת, כגון רכבת, מעלית או מכונת כביסה. ההצלחה הטכנית של מערכות אלו מפתיעה. ↩
ראה מאמרה של אסתר שינברג ב״מחשבות” 64, “המשמעות שמעבר לצלילים״, על האי ודאות במוסיקה. ↩









