הקדמה:

הנסיון המעשי שנרכש עד כה בתיכנות בבראייל למחשבים מורה בודאות, כי התוכניתן העיוור אינו נופל מעמיתו הפיקח מבחינת יכולתו ויעילותו. עם זאת, בעיה אחת חשובה מונעת שוויון מלא בין השניים והיא — ניצול זמן המחשב. מתברר שכתב הבראייל אינו הכתב האופטימלי בשביל המחשב, מאחר שלצורך ההדפסה בבראיל נזקק המחשב לזמן רב יותר (פי 10) מאשר בשפה הסימבולית הרגילה. כן נוצר ביזבוז ניכר של נייר ההדפסה עקב השמוש בכמה שכבות נייר במדפסת לצורך הטבעתן הברורה של בליטות הבראייל.
מר נחמן גבעולי, המתכנת הראשי של בנק לאומי לישראל, מנתח בעיה זו ומעלה מספר תחליפים לשפת הבראייל — יעילים וחסכוניים ממנה עד כדי 75%.
מר גבעולי זכה השנה בפרס קפלן, במשותף עם קבוצת מחקר לשיקום עיוורים ומוגבלים, על עבודתו והשגיו בנושא התיכנות לעיוורים.
כל אות בכתב בראייל תופסת 6 מקומות על הנייר, במלבן שגבהו 3 ורחבו 2. כל מקום כזה יכול להכיל נקודה, או להיות ריק. בס״ה יתכנו איפוא 64 אפשרויות שונות, החל בששה מקומות ריקים וכלה במלבן של שש נקודות —

למעשה כל האפשרויות מנוצלות, מאחר שממילא אין נוהגים להעניק למחשב, לצרכי הדפסה (גם בכתב רגיל), מספר כה גדול של אותיות וסימנים שונים.
העובדה שכל אות בכתב בראייל רחבה שני מקומות, ודרוש מקום נוסף כרווח בינה ובין האות הסמוכה, גורמת לכך שכל שורת הדפסה מתארכת פי 3 כשהיא מתורגמת לבראייל. נוסף להגדלת זמן ההדפסה וכמות הנייר הנצרך, יש בזה עוד חיסרון: המבנה של שורת ההדפסה אינו נשמר בזמן התרגום, והדבר גורם לקשיים בבדיקת הפורמאט של דוחות, למשל.
יש איפוא מקום לעיין באפשרות, שהאות בכתב העיוור לא תהיה במבנה של מלבן בן 3×2 מקומות, אלא במבנה אחר. נראה כי הטוב ביותר היה לתת לאות מבנה חד-ממדי מאונך, כי אז יסולק הצורך ברווח בין האותיות. כדי להשיג 64 אפשרויות שונות אפשר היה לקבוע שצורת האות היא מלבן זקוף בן 6×1 מקומות, החל בששה מקומות ריקים וכלה בשש נקודות, במאונך.
במקרה זה היינו חוסכים למעלה מ-40 אחוז מכמות הנייר הנצרכת, כי כל אות היתה תופסת רק 7 מקומות (ביחד עם הרווח שבין השורות) במקום 12 מקומות לפחות (ביחד עם הרווחים שבין האותיות ובין השורות).
ברם, אילו הרשינו לעצמנו להשתמש, מלבד בנקודה ובמקום ריק, גם במרכיב נוסף, כגון קו מאוזן, אפשר היה להסתפק באותיות קטנות עוד יותר. ארבעה מקומות, למשל, היו מאפשרים 81 צירופים שונים, שהם הרבה למעלה מן הדרוש. יכולים אנו איפוא להגביל את עצמנו ולקבוע, כי המקום העליון בכל אות יכיל רק נקודה או קו, אך אינו יכול להיות ריק. ע״י כך נצמצם את מספר האפשרויות ל-54 בלבד, אך נקל בזה על העיוור במציאת ״התקרה״ של השורה הבאה.
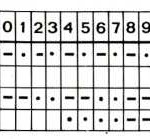
כדוגמה לכתב כזה אפשר להביא את כתב מורס, למשל, כשהוא כתוב במאונך:
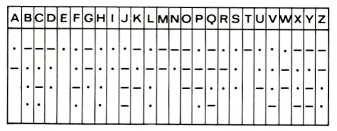
יתרונו הגדול של כתב זה (נוסף לעובדה שהוא כתב ידוע, ויתכן שהוא מוכר לעיוור מראש) הוא בכך, שאין בו מקומות ריקים בתוך האות, אלא רק בתחתיתה. אמנם, לגבי ספרות וסימנים מיוחדים נהיה נאלצים לוותר על כלל זה, ולסטות מן הקוד של מורס, כי הוא דורש יותר מארבעה מקומות. לגבי ספרות נוכל לקבוע, למשל, כי המקום השני בכל אות הוא תמיד ריק. לדוגמה:
הכלל הוא פשוט: נקודה במקום העליון ערכה 1; נקודה במקום השלישי ערכה 2; נקודה במקום התחתון ערכה 4; קו במקום התחתון ערכו 8; קו במקום הראשון או השלישי ערכו אפס, והוא נוסף רק כדי לא להשאיר באות חללים בלתי רצויים.
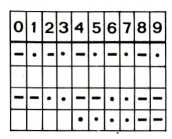
לגבי סימנים מיוחדים נוכל לקבוע את הכלל, כי המקום השלישי באות חייב להיות ריק. מאחר שהמקום העליון והתחתון חייבים להיות מלאים, נותן לנו כלל זה 12 סימנים מיוחדים. לדוגמה:
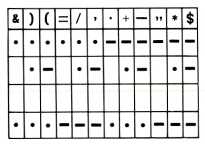
אם יש הכרח בכך, אפשר להוסיף עוד 6 אותיות, תוך ניצול האפשרויות שלא מוצו (כגון ארבעה קווים). החיסכון בכתב זה, אשר כל אות בו תופסת רק 5 מקומות במקום 12, הוא כמעט 60 אחוז.
השאלה, כמה ואילו סימנים שונים ניתנים להבחנה ע״י העיוור, אין לה כנראה תשובה החלטית אחת. הדבר תלוי לא רק בעיוור עצמו — דקות חוש המישוש שלו ומידת המאמץ שהוא מוכן להשקיע בתירגול בכתב החדש, אלא גם בדרך השימוש במדפסת. כדי לקבוע דברים אלה יש צורך לערוך ניסויים מבוקרים בתנאים שונים.
לצורך ההצעות דלקמן נצא מן ההנחה, כי העיוור יכול להבחין בין ארבעה סימנים שונים, כגון נקודה, קו מאוזן, אלכסון ומקום ריק. במקרה זה אפשר להסתפק בשלושה מקומות בלבד לכל אות — ארבעה ביחד עם הרווח שבין השורות — ולחסוך בכך כשני שלישים מתצרוכת הנייר. יתרון נוסף, חשוב מאד של שיטה זו הוא, שהיא יכולה להיות מבוססת על כתב בראייל הרגיל: כל זוג מקומות שכנים באות בראייל ייהפך למקום אחד באות החדשה, לפי המפתח הבא — שני מקומות פנויים ייהפכו למקום פנוי; נקודה ומקום פנוי ייהפכו לאלכסון; מקום פנוי ונקודה ייהפכו לנקודה; ושתי נקודות תיהפכנה לקו מאוזן. העיוור יוכל איפוא ללמוד את הכתב החדש ולקרוא אותו בקלות יחסית. להלן דוגמה לכמה אותיות בכתב החדש:
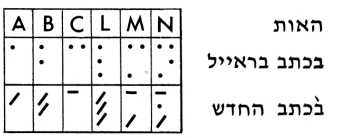
קיימת גם אפשרות אחרת. יתכן שהרצון להקל על העיוור את המעבר לכתב החדש אינו צריך להוות גורם מכריע, שהרי כל תכניתן חייב ממילא ללמוד כתבים שונים ושיטות מספריות חדשות. אפשר איפוא לבסס את הכתב החדש לפי שיטה אחרת, כגון לפי המבנה הפנימי, הבינארי, של האותיות בשפת המחשב. לפי שיטה זו נוכל לתת ייצוג לכל צירוף של תגים (״ביטס״) בינאריים, גם אם אין הוא ניתן בדרך כלל להדפסה רגילה, והעיוור יקבל איפוא כתב המצטיין בכך שהוא קוד שלם של המחשב, בדומה לכתב ההכסאדצימאלי, למשל, הנהוג לגבי מחשבי י.ב.מ. 360. יתרון נוסף לכתב כזה נעוץ בעובדה, שתכנית התרגום מכתב בראייל לכתב החדש תהיה בוודאי קלה ומהירה יותר, אם קיימת התאמה פשוטה בין המבנה הבינארי של האות ובין מרכיביה בכתב החדש, ובזה ייחסך זמן הדפסה, בנוסף לזמן הנחסך עקב ממדיה הקטנים של האות.
אם נתיחס אמנם למחשבי י.ב.מ. 360, שבהם מורכבת כל אות מ-8 תגים בינאריים, נצטרך להקציב לה לפי הצעה זו ארבעה מקומות. (במחשבי 1401 ו-1460 יספיקו שלושה מקומות). כאן כל זוג תגים סמוכים יתפסו מקום אחד באות, לפי המפתח הבא: שני אפסים ייוצגו ע״י מקום ריק; 1 ו-0 ייוצגו ע״י אלכסון; 0 ו-1 ע״י נקודה; 1 ו-1 ע״י קו מאוזן. אותן האותיות בכתב זה תיראינה כך:

כתב זה הריהו מקביל לגמרי לכתב ההכסאדצימאלי המקובל, שבו מיוצגת כל אות ע״י 2 סימנים, מתוך 16 סימנים שונים אפשריים. הסימנים השונים הם:
0123456789ABCDEF
כל סימן הכסאדצימאלי מתורגם בכתב הנ״ל לשני סימנים, כדלקמן (לפי אותו הסדר):

יוצא איפוא כי באותם המקרים, שהתכניתן מבקש הדפסה הכסאדצימאלית, עשוי הכתב הנ״ל, התופס 3 מקומות לאות (ביחד עם הרווח בין השורות), לעומת 12 מקומות בכתב בראייל רגיל, לחסוך 75 אחוז מתצרוכת הנייר! ברור כי כל חיסכון בנייר כרוך גם בחיסכון בזמן ההדפסה (בשיעור מקביל כמעט).
משום כך נראית לי הצעה אחרונה זו יותר מכל האחרות. הכתב הוא קל ללימוד, מאחר שהוא מבוסס על הכתב ההכסאדצימאלי, אשר התכניתן חייב ממילא להכיר. יתר על כן, הוא חוסך לעיוור את הצורך ללמוד את הכתב ההכסאדצימאלי בנוסף לכתב הזה. דבר זה, כאמור, טעון מחקר, שבו יש לקבוע, קודם כל, אילו הם הסימנים אשר קל ביותר לעיוור להבחין ביניהם.