הקדמה:
מחבר המאמר, פרופ׳ מיכאל רבין, מכהן מאז 1958 כמרצה ופרופסור למתמטיקה באוניברסיטה העברית בירושלים. את המאמר המתפרסם כאן עיבד פרופ׳ רבין על יסוד הרצאה שנשא במליאת הפתיחה של הכנס הארצי לעיבוד נתונים, באפריל השנה.
פרופ׳ רבין נולד בגרמניה, סיים את למודי העממי והתיכון בארץ וקיבל ב-1953 תואר מוסמך למתמטיקה באוניברסיטה העברית. את התואר השלישי, דוקטור למתמטיקה, השלים באוניברסיטת פרינסטון, ארה״ב, בה נשאר ללמד בין השנים 56—58.
בעשר השנים האחרונות שהה פרופ׳ רבין פעמים אחדות באוניברסיטאות יאל, ברקלי ומ.י.ט. כפרופסור אורח. במקביל לכך שימש גם יועץ מחקר לחברת י.ב.מ. ולחברת בל.
ב-1960 הוענק לפרופ׳ מיכאל רבין פרס ויצמן למדעים מדויקים על עבודתו בלוגיקה מתימטית ובתורת אוטומטים.

עידן המחשבים, הנכנס כעת לעשורו השלישי, צופן לנו שינויים מסויימים בשיטות, במטרות ובבעיות העומדות לפנינו. ברצוני לדון על כמה מן האימפליקציות המדעיות הנובעות מתמורה זאת שבפתח.
מבחינות מסויימות מתקרבת טכנולוגית המחשבים, במידה שהיא טכנולוגיה של מרכיבים פיסיקליים שונים, למיצוי. מהירויות מרכיבי היסוד של המחשב, המבצעים את פעולות המיתוג והזכרון, מתקרבות למהירויות ההולכה של זרמים חשמליים בתוך החוטים. משמע, שהזמן הדרוש לביצוע הפעולות היסודיות במחשב מתקרב מבחינת סדר הגודל לזמן ההולכה של הפולס החשמלי מנקודה אחת לנקודה שניה בתוך המחשב. פירוש הדבר, שאף כי עשויים אנו לשכלל ולהחיש את מהירות המיתוג, מביאה אותנו מיגבלת ההולכה סמוך למיגבלות האבסולוטיות של פיתוח טכנולוגית המחשבים.
אחד מכיווני ההתפתחות בתחום של החשת המהירות הוא מגמת הזיעור (miniaturization) של המרכיבים החשמליים, שתכליתה לצמצם את המרחקים ההדדיים בתוך המחשב. כיוון התפתחות אחר, חשוב ביותר, הוא בניית זכרונות גדולים וזולים. בתחום זה נעשים נסיונות שונים, כמו יישום תופעות העל-מוליכות. אולם, כללית ניתן לומר, כי בעוד בעבר פותחו אחת לכמה שנים מחשבים חדשים שהיו מהירים פי עשרה או פי מאה מקודמיהם, הרי בעתיד אין אנו יכולים לצפות לשינויים מהותיים כאלה בגלל המיגבלות הטכניות שהזכרתי.
עובדה זאת מעמידה את המחקר בתחום המחשבים לפני מפנה מסויים. אם עד כה היו השאלות היסודיות — מה אפשר לבצע בעזרת מחשב וכיצד, תהיה מעכשיו השאלה היסודית — מהי הדרך היעילה ביותר לביצוע חישוב, או עיבוד, מסויים של נתונים.
שינוי זה בדגש הוא פועל יוצא של התפתחות המחשבים. בראשית הדרך התבטא החידוש הגדול ביותר בעצם העובדה שיכולים אנו לבנות מחשב עם תכנית אגורה (stored program), המאפשרת לו לפקח על פעולותיו שלו ולבצע חישובים מסובכים ביותר ללא התערבות יד אדם. בשלב זה היה, כמובן, הדגש על ביצוע הדברים, כשהמטרה היא לגלות את האפשרויות הגנוזות בכלי11 זה. עיקר המאמץ הוקדש לכתיבת תכניות לצרכי חישובים מסובכים, שאיפשרו לפתור בעיות שונות בפיסיקה תיאורטית, בהנדסה וכיו״ב בעיות שלא ניתן היה לגשת אליהן לפני שפותח המחשב. הצלחה מרשימה אחרת קצר המחשב בתחום של עיבוד נתונים, בנושאים שונים ומגוונים, כמו : חישוב משכורות, רישום מלאי ועוד. עם זאת, בצד ההצלחות הגדולות לא חסרו גם כשלונות ובמיוחד אכזבות. התקווה התמימה שליוותה את המחשב בראשית דרכו, כאילו עתיד הוא לפטור אותנו מכמות ניכרת של עבודה מחשבתית יוצרת — נתבדתה. אולי הדוגמה הטובה ביותר לכשלונו של המחשב הוא בשדה התרגום המכאני, נושא שההתקדמות בו מפגרת בהרבה אחרי הציפיות.
כיום, לאחר שטכנולוגיית המחשבים מתקרבת, כאמור, למיצוי, מוסט דגש המחקר לניתוחם המדוקדק של תהליכי החישוב, למען נוכל לנצל אותה טכנולוגיה העומדת לרשותנו בצורה היעילה ביותר. אם נמצא את הדרך היעילה ביותר לביצוע חישוב מסוים, הרי שנוכל להגדיל את היקף החישובים והביצועים — עד תחום המיגבלות האבסולוטיות של מכשיר זה המצוי בידינו.

חזרה לשאלות יסוד
הבה נבחון את הדבר. אחת היחידות המרכזיות במחשב היא, כידוע, היחידה האריתמטית, המבצעת את פעולות היסוד של חיבור, חיסור, השוואה (של שני מספרים) וכן כפל וחילוק. ליחידה האריתמטית תכנון מקובל ומהירות מסויימת בה היא מבצעת את הפעולות האריתמטיות. מהירות זאת, התלויה בפעולת המתגים, אין אנו יכולים, כאמור, להחיש באורח ניכר. כיוון שכך עולה שאלה עקרונית: האם המעגלים המתוכננים הם המעגלים היעילים ביותר, או שנוכל ע״י תיכנון מוצלח יותר להחיש את זמן החיבור והחיסור במחשב?
נניח כי ברצוננו לחבר שני מספרים בעלי n ספרות בשיטה בינארית. בטכנולוגיה הרגילה של מחשבים עשוי n להיות 32. מספרים אלה יופיעו על רג’יסטרים ואילו התוצאה תופיע על רג’יסטר הסיכום.
בביצוע המקובל של פעולת חיבור קיימת שארית, הנודדת מהסיפרה הימנית של המחוברים ועוברת שמאלה אל הסיפרה הראשית. מכאן, שאם משך זמן הפעולה היסודית של צרוף שתי ספרות לסיפרת סיכום ולסיפרת שארית הוא t, כאשר t הוא מספר קטן התלוי בטכנולוגיה בה אנו משתמשים, הרי שהזמן הדרוש לחיבור שני המספרים הוא n•t.
מכאן נובעת השאלה : האם אפשר לשפר זמן זה על-ידי ארגון מוצלח יותר של המעגל ? בלי להכנס לפרטים נאמר כאן, כי אכן, ע״י תכנון מחוכם אפשר להגיע, לזמן t•log2n. במקרה זה נקבל, איפוא, 5 יחידות זמן במקום 32.
נעבור עכשיו לשאלה הבאה : אם הצלחנו להוריד את מהירות החיבור מ-t•n ל-t•log2n, מנין לנו שאי-אפשר להוריד בסדר גודל נוסף את מהירות החיבור ע״י תכנון מחוכם יותר ?
התשובה היא לא. כי מתברר שאפשר לנסח בעיה זאת בצורה מתימטית מדוייקת לחלוטין ולהיווכח ש-t•log2n הוא הדבר הטוב ביותר שאנו מסוגלים לעשותו.
החישוב במקביל
כיוון אחר שאנו יכולים לחקור כדי להגיע לשמוש המירבי והמשוכלל ביותר של המכשירים המצויים בידינו — הוא החישוב במקביל (פאראלליזם).
הפילוסופיה מאחורי שיטה זו ברורה. אם אין בידינו להחיש את מהירות החישוב של מחשב בודד, הבה נפעיל מספר מחשבים — או מספר יחידות אריתמטיות באותו מחשב — במקביל, על אותה בעיה המעסיקה אותנו.
במעשה אין הדבר ברור כל-כך. מסתבר שבתחום החישוב במקביל מתעוררות בעיות מתימטיות מענינות ביותר. כל עוד מדובר, לדוגמה, על חיבור טורי מספרים, יבצעו אמנם שתי יחידות אריתמטיות את החיבור במחצית הזמן שנדרש היה ליחידה אריתמטית אחת. אולם, רוב החישובים המענינים יותר הם כאלה, שכדי לבצע את הצעד הבא אנו זקוקים לתשובה של הצעד הקודם. הבה נעקוב אחרי תהליך הפתרון של משוואה נומרית, 0=(f(x, בעזרת שיטת קירוב. תחילה פותחים ומוצאים קירוב ראשון, x1, שהוא כמעט פתרון. ובודקים במובן מסויים עד כמה הוא קרוב לפתרון. אח״כ אנו מטפלים ב- x1, משכללים אותו ומוצאים את x2, הקרוב יותר לפתרון המשוואה. ורק אחרי שיש לנו את x2 נוכל לגשת לחישוב x3, שהוא קירוב טוב עוד יותר.

במקרה זה אנו רואים, איפוא, כי אין לנו תועלת רבה מהחישוב במקביל, מאחר שלא נוכל לגשת לחישוב x2 בטרם נדע מה היה x1, ובודאי לא ל-x3 לפני שנדע מהו x2, וכך חוזר חלילה.12
אמנם, אין החישוב במקביל נעדר כל תועלת גם במקרה זה, לפי שהוא מסוגל להחיש את חישובי הביניים. אך ברור שכדי להגיע ליעילות גבוהה יותר עלינו להקדים ניתוח עמוק יותר של החישובים שאנחנו רוצים לבצע.
בעיות דומות מתעוררות בבואנו ליישם את שיטת החישוב במקביל לפתרון משוואות דיפרנציאליות, או לתהליכים של עיבוד נתונים. גם אלה בעיות מסוג חדש שלא חשבו עליהן קודם.
נכון, אנשים הרבו לעסוק בשיטות של חישוב מקורב גם לפני פיתוח המחשבים, אך בעיות אלה לא התעוררו אז כיוון שהמחשב האנושי — האיש שעורך חישובים — ממילא אינו יכול לערוך חישובים במקביל. שאלת החישוב במקביל הוא פועל יוצא של מכשירי החישוב.
דוגמה יפה לבעיה מתימטית, המתעוררת בעיבוד נתונים, הוא תהליך המיון של מספרים לפי סדר גודל (Sorting).
אחד היישומים המובהקים של תהליך זה, באמצעות מחשב, נעשה בחישובי מס-הכנסה בארה״ב. לכל אדם צמוד מספר הביטוח הלאומי וכל תשלום הנזקף לזכותו מצורף אליו מספרו.
אינפורמציה זו מועלית במשרדים האיזוריים על סרטים מגנטיים, אשר נשלחים למרכז בוואשינגטון. במרכז נרשמים התשלומים השונים בתיקו האישי של הנישום, כדי שכל דולר ששולם לו יובא בחשבון, כמובן, במס-הכנסה שלו. תהליך זה מחייב עריכה מוקדמת של האינפורמציה לפי סדר מספרי הביטוח הלאומי, לפי שרק בדרך זו אפשר לשלב אותה בתיקים הקבועים המצויים במרכז.
כלומר, הכרח הוא למיין מיליונים רבים של מספרים בסדר הטבעי שלהם, פעולה המצריכה שעות רבות ויקרות של זמן מחשב.
תהליך מייגע זה הביא חוקרים שונים לשאול את עצמם אם השיטות והתכניות הקיימות למיון הן באמת הטובות ביותר מבחינת זמן הביצוע וכמות המיכשור הדרושה. שאלה זו, מהן האסטרטגיות האופטימליות למיון, ניתנת לביטוי במונחים מתימטיים, כך שאפשר לערוך חישובים מתימטיים מדוייקים המשווים שיטות מיון שונות.
חשיבותה המעשית של שאלה מתימטית זו ברורה. שכן, די אם נצליח לקצר את זמן החישוב בעשרים אחוז בלבד; הרי בשל היקפה הגדול של העבודה, נקבל חסכון כספי ניכר.
מקרה אחר הנזקק לניתוח מתימטי כדי לשכלל את השיטות הקיימות, הוא כאשר כמות הנתונים לעיבוד מגיעה לנקודת התפוצצות — שאין להתגבר עליה בעזרת המכשירים העומדים לרשותנו. טפול מתימטי נבון יאפשר לנו להכניס את הבעיה למיטת סדום של מיגבלות הטכנולוגיה הנתונה לנו.

חישובי פולינומים ומטריצות
נחזור לתחום החישובים המדעיים עם שתי דוגמאות הנוגעות לחישובים אלגבריים.
פולינום (רב-איבר) ממעלה n הוא ביטוי מהצורה : f(x)=an+an-1+…+a0 כאשר a0,…,an הם מקדמים מספריים נתונים.
נניח שברצוננו להציב ב-(f(x מספר b ולחשב את הערך (f(b. עיון פשוט מראה לנו, כי נוכל לעשות זאת על-ידי n פעולות כפל ו-n פעולות חיבור. מיד מתעוררת השאלה — האם דרך זו היא החסכונית ביותר? מענין לציין כי המתמטיקאי הידוע אוילר (Euler) כבר טיפל בנושא זה לפני 200 שנה במקרה של 4=n. ניתוח מתימטי מראה שאכן כך הדבר, והדרך האופטימלית היא הדרך הידועה לנו.
אבל ראוי לציין, כי אמנם כך הדבר כאשר מדובר על הצבה חד-פעמית בתוך פולינום. שכן, אם מדברים על פולינום שמוצבים בו הרבה מספרים — המצב שונה במקצת. אך זהו ענין טכני שלא ניכנס לפרטיו.
הדוגמה השניה נוגעת להכפלת שתי מטריצות, בנות n שורות ועמודים, זו בזו. למשל, מטריצה מסדר 2 על 2 היא מערכת
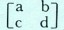
ואם ברצוננו להכפילה ב-
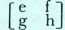
הרי, לפי ההגדרות, התוצאה היא :
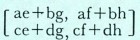
במקרה הכללי של מטריצות מסדר n על n אנו זקוקים בשיטה המקובלת ל-n3 פעולות חיבור ו-n3 פעולות כפל. בחישובים הקשורים לתכנון ליניארי, או לבעיות של פיסיקה תיאורטית, תדירים המקרים בהם אנו מטפלים במטריצות גדולות — נומר, מסדר 100 על 100.
מדובר כאן, אם כן, על מיליון פעולות חיבור ומיליון פעולות כפל. ושוב מתעוררת השאלה — האם זהו הדבר האופטימלי שבידינו לעשות ?
בטרם נשיב על כך נביא ספור קצר מתוך האוטוביוגרפיה של דארוין. דארוין אמר, כי על איש המדע לבצע מפעם לפעם נסיון הנראה כבלתי הגיוני לחלוטין. אם הנסיון לא יצליח — אזי לא קרה דבר, אבל אם יצליח ותתקבל תוצאה בלתי צפויה — תהא זאת תגלית ממדרגה ראשונה. דארוין מספר על עצמו שב13אותו בוקר ניסה הלכה למעשה תיזה זאת, בכך שניגן בחליל אל פרחיו. הוא חיכה קמעה, אבל לא קרה דבר.
לא כך קרה כאשר טיפלו בשאלת כפל המטריצות. כאן נכונה לנו הפתעה. התברר שכדי להכפיל שתי מטריצות מסדר n על n – זו בזו, אפשר להסתפק ב-n3/2 פעולות כפל ו-3/2•n3 פעולות חיבור. מאחר שברוב המחשבים מהירה פעולת החיבור באופן ניכר מפעולת הכפל, נמצא ששיטה חדשה זאת מאפשרת החשה משמעותית של כפל מטריצות. בנסויים שנערכו עם האלגוריטם החדש פחת זמן החישוב כדי מחצית הזמן המקובל.

שמושים נוספים
נזכיר מספר תחומי פעולה נוספים בהם שיטות המחקר הן, חלקית לפחות, מתימטיות.
מחקרים מענינים נעשים בתחום כתיבת תוכניות העושות את המחשב כלי-עזר מצוין לאיש המדע היוצר. תוכניות אלו משתייכות לתחום הקרוי עירוך סמלים (Symbol manipulation). מתמטיקאי העוסק בפתרון בעיה מתימטית קשה עשוי תוך כדי עבודתו להזדקק להכפלת שני פולינומים זה בזה. עבודה זו, כאשר היא מתנהלת בעפרון ונייר, היא ממושכת מאד ומועדת לטעויות חישוביות.
מטרת המחקרים הנערכים בשטח זה היא לאפשר למתמטיקאי להדפיס את שאלת החישוב ישר על מכונת הכתיבה הקשורה למחשב, כך שיקבל את התשובה הנכונה בו-בזמן, כמעט.
בצורה דומה נוכל להעביר למחשב שאלות גיאומטריות במרחב רב-מימדי. שאלות שעוסקות במצבם ההדדי של מישורים וישרים במרחב חמש-מימדי הן מעבר ליכולת הדימוי החזותי של בן-אנוש, אך ניתנות לטיפול מהיר ומדוייק בעזרת מחשב.
תחום אחר בו משקיעים כיום מאמץ רב הוא יישום המחשב ככלי עזר בהוראה וחינוך. אפשר להבין את הטעם למאמץ הגדול אם נתבונן בפוטנציאל האדיר שיש ליישום זה בשוק. באוניברסיטה סטנפורד, לדוגמה, עובדים כיום על תכנית שתפקידה לסייע לתלמידי תיכון בפתרון בעיות של גיאומטריה אוקלידית. תוכנית זו תסייע לתלמיד, בין השאר, לבנות את השרטוט הגיאומטרי הנכון על מסך היחידה הטלביזיונית שקשורה למחשב.
מחשבי העתיד
נקדיש עתה כמה מלים על התוכניות לעתיד הקרוב והרחוק לפיתוח המחשבים ועל הבעיות המתימטיות הכרוכות בכך.
כיוון אחד, בו עתידים להשקיע מאמצים רבים בעתיד הקרוב, הוא בלי ספק — החישוב במקביל. נושא אחר, רב תמורות, הוא שיטת שיתוף זמנים (Time Sharing) כלומר, חלוקת זמן המחשב בין מספר משתמשים.
השימושים עליהם דיברנו קודם יתבצעו, אל-נכון, במסגרת שיתוף-זמנים. זה באשר לטווח קצר. לטווח ארוך יותר חושבים על מחשבי-ענק שיעסקו בארגון עצמי. הכוונה למחשבים שיכילו איזורים ומעגלים שלמים בלתי מחוברים ובלתי מאורגנים, אשר יחוברו ויאורגנו ע״י המחשב עצמו תוך כדי עבודה, בהתאם לבעיה אשר עליו לפתור. בשאלות אלה של ארגון עצמי טיפלו כבר בהרחבה באופן מתימטי טהור במסגרת הנושא : Self Reproducing Machines.
אין אמנם לומר בודאות, כי למחקרים אלה שמוש בלתי אמצעי לדברים שיעשו בעתיד, אך ודאי הוא, שטמונים בהם השלכות ורעיונות שאפשר לשאול אותם מהתורה המתימטית ליישומים.
נושא מרכזי וחשוב אחר הוא ההירארכיה של שפות תיכנות. כבר היום בונים הלכה למעשה שפות תיכנות, הפורטראן — למשל, המתורגמות אוטומטית ע״י המחשב לשפת המכונה. קיימות גם שפות נסיוניות משוכללות יותר שמספר שלבי הבינים מגיע, במובן מסוים, לשלושה. כעת מסתמנת נטיה לחקור תופעה זאת באופן שיטתי, כשהמטרה ליצור הירארכיות שיאפשרו לנו לכתוב תוכנית בשפה א׳, ואילו המחשב יתרגם אותה לשפה ב׳, ושפה ב׳ לג׳ וכן הלאה, לפי הצורך — עד לשפת המכונה.
הטיפול בשאלות אלה קשור באורח אמיץ בבעית הסמנטיקה של שפות תיכנות — נושא עמוק ורחב הנמצא עדיין בחיתוליו. נושא קרוב לזה, בו מתנהלת עבודה אינטנסיבית, הוא הבדיקה האוטומית של התוכניות (De bugging). המטרות הנוכחיות כאן צנועות יותר. עובדים, למשל, על שאלה של בדיקת הוכחות מתמטיות בעזרת מחשב, אך הכוונה היסודית היא להגיע לשאלה של בדיקת תוכניות בעזרת מחשב. לסיכום ניתן לומר, כי פיתוח המחשב לא רק הביא להישגים טכנולוגיים עצומים, אלא גם האציל התחדשות על שטחים מסוימים של המתמטיקה. כוונתנו לאותו תחום של המתמטיקה השמושית אשר אינו עוסק, כפי שהיה מקובל עד היום, בשאלות של זרימה, הידרודינמיקה, משוואות נומריות וכו’, אלא עוסק בבעיות קומבינטוריות, שפות מלאכותיות ותהליכי חישוב.
אין ספק, כי בד בבד עם הפיתוח הטכנולוגי, יבוא גם פיתוח תיאורטי נרחב בתחומים שמנינו. • •14





