הקדמה:
פרופ’ שמואל וינוגרד (36), יליד הארץ, סיים בית ספר תיכון בתל-אביב. לאחר שרות צבאי השלים תואר ראשון ושני בהנדסת חשמל ב-.M.I.T ארה״ב. ב-1961 הצטרף לחברת י. ב. מ. ועבד כחוקר במעבדות המחקר של י. ב. מ. ע״ש וואטסון בארה״ב. במקביל לעבודתו השלים תואר שני ושלישי במתמטיקה באוניברסיטת ניו-יורק. עבודת הדוקטור שלו עסקה בנושא הקרוי מורכבות חישובית. פרופ’ וינוגרד פיתח נוסחאות המאפשרות לחזות מראש מהו הזמן המינימלי שנדרש לביצוע פעולות כפל וחיבור של שני מספרים. באמצעות נוסחאות אלו ניתן לקבוע מה תהיה מהירות התקרה של מחשב כלשהו — בין קיים ובין בתיכנון — בביצוע פעולות חיבור וכפל.
למן שנת 1967 המשיך פרופ’ וינוגרד לעסוק ברציפות בתחום המורכבות החישובית, שעיקרו ניתוח הגורמים המעורבים בפעולת חישוב כלשהי, כגון: מספר פעולות הכפל או החיבור המצויות בעבודת חישוב נתונה. מטרת המחקרים הללו היא להגיע לידיעה מדוקדקת של יסודות החישוב הבסיסיים המצויים בפעולות חישוב מתמטיות, וע״י מחקר זה לפתח ולחדד את האינטואיציה של המתמטיקאי בבואו להעריך את מצבן ומעמדן של בעיות שטרם נפתרו. לכל המחקרים האלה השלכה ישירה על המחקר והפיתוח של המחשבים האלקטרוניים. לפני שנתיים מונה פרופ’ וינוגרד לעמוד בראש המחלקה למתמטיקה שבמעבדות המחקר של י. ב. מ.
בראשית שנה זו הוענק לפרופ׳ וינוגרד תואר ״עמית י. ב. מ. ״ מטעם הנהלת החברה בניו יורק. תואר זה, ששותפים לו 30 איש בלבד ברחבי העולם, מוענק לחוקרים ואנשי מדע של י.ב.מ. אשר רשמו לזכותם הישגים יוצאים מן הכלל בתחום המחקר המדעי.

לפני מספר שנים הזדמן לי לשוחח עם ד״ר הרמן גולדשטיין על בעיות מתמטיות הקשורות בתכנון מחשבים. ד״ר גולדשטיין היה בזמנו אחראי, יחד עם ד״ר פון נוימן, לבניית המחשב האלקטרוני הראשון באוניברסיטת פרינסטון. אגב השיחה שאלתי את ד״ר גולדשטיין מה היתה העבודה המדעית שהשפיעה עליהם ביותר בתכנון המחשב. ללא היסוס השיב שהיה זה מאמרו של א. מ. טיורינג, אשר בו הציג וניתח מה שקרוי היום מכונות טיורינג. כדי להבין את חשיבות התרומה שתרם מאמרו של טיורינג לפיתוח המחשבים האלקטרוניים, עלינו לזכור שהמחשב שנבנה בפרינסטון, במחצית שנות הארבעים, מהווה אב־טיפוס למחשבים שנבנו מאז, וכי כיום, לאחר יותר ממחצית יובל, משתמשים בעקרונות הבסיסיים שפותחו ע״י פון ניומן וגולדשטיין.
הפרדוקסים המתמטיים שהתגלו בסוף המאה שעברה ובתחילת המאה הנוכחית הטרידו לא מעט את המתמטיקאים ונתנו דחיפה למחקר מתמטי בשטח המכונה13 יסודות המתמטיקה. מחקר זה הראה שאי אפשר להסתפק בידיעה אינטואיטיבית של מהי קבוצה, מהי הוכחה ומהו תהליך חישוב, וכי נחוץ להגדיר מושגי יסוד אלה של המתמטיקה בדיוק רב, אחרת יש סכנה שיתקבלו פרדוקסים.
אחד החוקרים החשובים בשטח זח היה המתמטיקאי־לוגיקן האנגלי א. מ. טיורינג (1912־1954). ב־ 1937, בהיותו באוניברסיטת קמברידג׳ (קינגס קולג׳), פרסם טיורינג את תוצאות מחקרו על מספרים הניתנים לחישוב. המפליא בדבר הוא שלתוצאות מחקר זה, שהיה בזמנו אחד התיאורטיים ביותר והפחות שמושיים בתחום המתמטיקה, היו השפעה עמוקה ביותר על פיתוח מחשבים. ולמחשבים, כידוע, יש השלכות שימושיות ביותר על חיינו.
הבעיה שעמדה בפני טיורינג היתה כיצד להגדיר בדיוק מה שקרוי שיטת חישוב, או אם להשתמש במושג המתמטי: מה הוא אלגוריתם ומה ניתן לחשב ע״י אלגוריתמים. שיטות חישוב לבצוע פעולות מתמטיות ידועות לכולנו עוד מלמודי המתמטיקה בבית הספר היסודי. למדנו כיצד לחבר שני מספרים באורך כלשהו, כאשר נידרש מאתנו לשנן רק מהו סכום שתי ספרות. בעזרת האלגוריתם לחיבור, ואחרי שינון לוח הכפל של מכפלת שתי ספרות אחת בשניה, למדנו שיטה להכפלת שני מספרים כלשהם; כמו כן יודעים אנו אלגוריתם המאפשר לנו לחלק שני מספרים אחד בשני. מאוחר יותר, בבית הספר התיכון, הציגו לנו את האלגוריתם של אוקליד למציאת המחלק המשותף המקסימלי של שני מספרים (המספר הגדול ביותר המחלק את שניהם).
אפשר להצביע על מספר תכונות משותפות לכל שיטות החישוב שהוזכרו עד עתה, המאפיינות את מה שאנו מכנים אלגוריתם. הראשונה היא שכמות האינפורמציה שעלינו ״לזכור״ לביצוע החישוב היא קטנה יחסית; לחיבור שני מספרים עלינו לדעת מהו סכום שתי ספרות, וכן לזכור אם תוצאת הצעד הקודם היתה גדולה מ־9. התכונה השניה היא שאת החישוב מפצלים לפעולות אלמנטריות החוזרות על עצמן — כל אחת מהן פשוטה ביותר. באלגוריתם החיבור עלינו לחבר תחילה את שתי הספרות הימניות וכך אנו מקבלים את סיפרת היחידות של הסכום, אח״כ צריכים לחבר את שתי הספרות הבאות משמאל (ולהוסיף להן 1 אם התוצאה הקודמת היתה גדולה מ־9); וכך אנו מקבלים את סיפרת העשרות של הסכום. תכונה שלישית, שנראית כל כך פשוטה עד כי כמעט אין חושבים עליה, היא שתהליך החישוב הוא כזה שהמבצע יודע באופן ברור ומידי מתי הסתיים החישוב.
מכונת טיורינג בפעולה
הבעיה שעמדה בפני טיורינג, כאמור, היתה כיצד להקנות משמעות יותר מדויקת למונחים די מעורפלים, כגון ״זכירת כמות אינפורמציה קטנה״ ו״פעולות אלמנטריות״, שהשתמשנו בהם על מנת לאפיין אלגוריתם; שכן, רק לאחר קביעת המשמעות המדוייקת למושגים אלה אפשר לחקור מה ניתן לחישוב ומה לא. מאחר שכל אחד מהאלגוריתם הנ״ל משמש לפתרון אינסוף בעיות מאותו הסוג (למשל, חיבור כל זוג מספרים או כפל כל זוג של מספרים) אנו רשאים לוותר על הדרישה שכמות האינפורמציה שצריכים לזכור ומספר הפעולות השונות יהיו ״קטנות״, אבל נעמוד על כך שכמויות אלה הן סופיות, גם אם במקרים מסוימים הן גדולות מאד. הבעיה היותר קשה היא לתת תאור מדויק למה אנו מתכוונים בדברנו על ״כמות אינפורמציה סופית״ ו״צעדים אלמנטריים״.
במאמר שפורסם ב־1937, בעתונה של החברה המתמטית של לונדון, הציע טיורינג תאור של מכונה לביצוע חישובים כלשהם. סוג כזה של מכונה זכה להקרא בהמשך על שמו: ״מכונת טיורינג״. נתאר לעצמנו מכשיר היכול להמצא במספר סופי של מצבים (כמו, למשל, המצבים של מוט ההילוכים במכונית). מכשיר זה ״מתהלך״ לאורך סרט המחולק למשבצות, שעל כל אחת מהן יכולה להיות רשומה סיפרה (או אות או סימן פיסוק). בכל עת ועת ״מתבונן״ המכשיר בסימן הרשום במשבצת אחת — אליה הוא מכוון. בהתאם למצב שבו נמצא המכשיר באותו רגע ולסיפרה הרשומה על המשבצת מגיב המכשיר באחת (ורק באחת) משלוש התגובות הבאות:
1. הוא משנה את הרישום במשבצת (בין השאר הוא יכול למחוק את הרישום)
2. הוא זז משבצת אחת ימינה
3. הוא זז משבצת אחת שמאלה.
יחד עם ביצוע אחת מפעולות אלה ״מחליט״ המכשיר, על סמך הכתוב במשבצת והמצב בו הוא נמצא, על מצבו החדש.
החישוב המעשי נעשה בצורה הבאה. על סרט (שאותו אפשר להאריך לכל צד כרצוננו) נרשמת הבעיה אותה רוצים לפתור; כלומר במספר משבצות נרשמות ספרות. מציבים את המכשיר מול הסיפרה הראשונה משמאל, מכניסים אותו למצב מסוים, הנקרא ״המצב ההתחלתי״, ומפעילים את המכשיר; כלומר נותנים למכשיר לבצע את הפעולות הנ״ל. הוא זז לאורך הסרט ימינה, שמאלה, כותב ומוחק ספרות; פעולה זו נמשכת עד שהמכשיר נכנס למצב מסוים הנקרא ״מצב סופי״, בהגיעו למצב זה הוא נעצר והרישום המצויין על הסרט ברגע זה הוא תוצאת החישוב. למה הדבר דומה? למכונית בעלת 4 הילוכים אוטומטיים, אשר מהירותה, כיוון נסיעתה, מועד החלפת ההילוך וגם עצירתה תלויים בשני גורמים: בהילוך שבו נמצאת המכונית (בהשאלה — המצב בו נמצאת מכונת טיורינג) ובשיעור הלחץ של הנהג על דוושת הדלק (בהשאלה — הסיפרה שמכונת טיורינג קוראת ברגע מסויים).
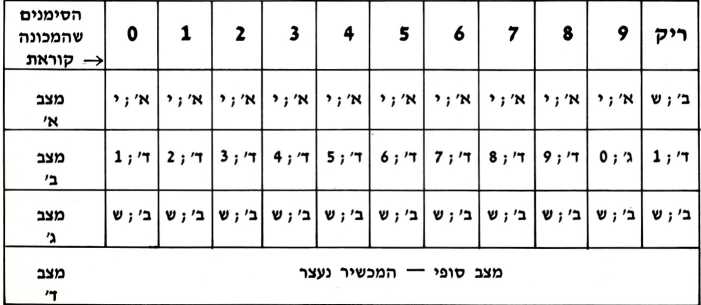
נעיין אם כן במכונת טיורינג בעלת 4 מצבים ונצייר טבלה אשר תתאר מראש את תגובותיו של המכשיר בכל מקרה ומקרה. לטבלה 4 שורות — שורה עבור כל מצב, ו־11 עמודות — עמודה עבור כל סיפרה (מאפס עד תשע) ועמודה נוספת שתציין את תגובת המכשיר למקרה שהמשבצת אותה הוא קורא הינה ריקה.
נתבונן עתה בטבלת התגובות וננסה את פעולתה. נניח שהמכשיר נמצא במצב א׳ והוא ״קורא״ את הסיפרה 3. בהצטלבות של השורה מצב א׳ עם העמודה של הסיפרה 3, מופיע הרישום א'; י שהוראתו: עבור למצב א׳ (במקרה זה נשאר באותו מצב) וזוז משבצת אחת ימינה (י=ימינה).
אם המכשיר נמצא במצב א׳ והמשבצת אותה הוא ״קורא״ היא ריקה, אז, בהתאם לכתוב בטבלת התגובות, עליו לזוז משבצת אחת שמאלה (ש=שמאל) ולעבור למצב ב׳. אבל אם המכשיר נמצא במצב ב׳ ו״קורא״ את הסיפרה 5 עליו ״לכתוב״ במקומה את הספרה 6 ולעבור למצב ד׳, שהוא מצב הסופי בטבלה זו, ובהגיע אליו המכשיר הוא נעצר (מצב א׳ הוא המצב ההתחלתי).
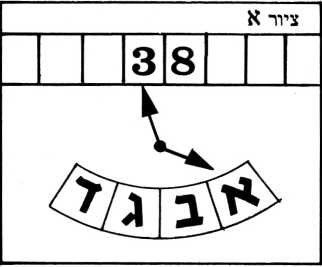
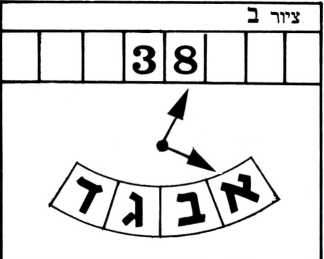
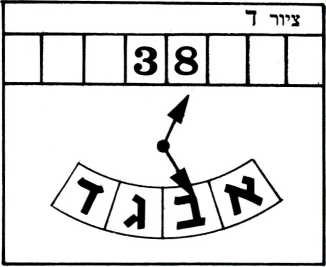
עתה אנו יכולים לבחון את הפעולה של מכונת טיורינג הלכה למעשה. נניח שאנו רושמים על הסרט את המספר 38. המכשיר נמצא במצב ההתחלתי, מצב א’, ו״קורא״ את הסיפרה 3 (ראה ציור א׳) טבלת התגובות מראה שעל המכשיר לזוז משבצת אחת ימינה ולהשאר במצב א׳; משיבצע הוראה זו ימצא המכשיר במצב א׳ ויקרא את הסיפרה 8 (ראה ציור ב׳). בצעד השני, על פי טבלת התגובות (נקודת ההצטלבות של מצב א׳ עם עמודה 8) עליו להשאר במצב א’ ולזוז שוב משבצת אחת ימינה. וכך אמנם יעשה.
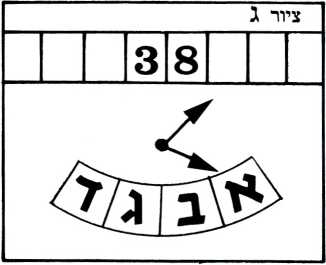
אלא שעתה הוא ״קורא״ משבצת ריקה (ראה ציור ג׳) ועל פי טבלת התגובות (נקודת ההצטלבות של מצב א׳ עם עמודה ״ריק״) עליו לזוז משבצת אחת שמאלה ולעבור למצב ב׳ (ראה ציור ד׳).
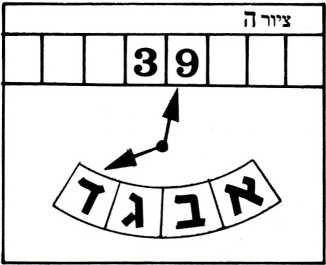
מה אומרת לנו טבלת התגובות? רשום 9 במקום 8 ועבור למצב ד׳, שהוא כידוע לנו המצב הסופי. המכשיר עוצר את פעולתו ועל הסרט מופיע המספר 39 תחת המספר שהיה רשום עליו קודם תחילת הפעולה (ראה ציור ה׳), וזו תוצאת החישוב. (הקורא מוזמן לנסות כוחו במספר ״פרובלמטי״ יותר, כמו 99).
ממהלך הפעולה שהדגמנו לעיל מתברר אל נכון, כי מכונת טיורינג המסויימת שתיארנו כאן מבצעת את הפעולה של הוספת יחידה אחת לכל מספר שיהיה רשום על הסרט בתחילת הפעולה.
המכונה האוניברסלית
התיאור המפורט של המכונה נעשה במתכוון כדי להדגיש את פשטות התהליך. הדרישה שכמות האינפורמציה שצריכים לזכור היא סופית מתבטאת במספר הסופי של המצבים, וברור שכל צעד וצעד של מכונת טיורינג הוא פשוט. המפתיע בדבר הוא, שכל מה שניתן לחשב ע״י תהליך חישוב כלשהו ניתן לחשב גם ע״י מכונת טיורינג. כלומר, בשביל כל תהליך חישוב יכולים אנו לתאר לנו קופסה קטנה, המכילה מספר סופי של הוראות אותן יכולה היא לבצע. הקופסה ״מטיילת״ לה על סרט — פעמים ימינה ופעמים שמאלה — מוחקת ורושמת ספרות וכשהיא נעצרת, רשומה התוצאה על הסרט.
אלו מבין הקוראים שיש להם ידיעה במחשבים עמדו כבר קרוב לודאי על הקשר בין מכונות טיורינג למחשבים. שכן המכשיר עם תגובותיו אינו אלא הפשטה של יחידת העיבוד המרכזית (CPU) — אותו חלק של המחשב בו נעשות הפעולות האריתמטיות והלוגיות; הסרט על משבצותיו הוא הפשטה של הזכרון, ואילו המספר הרשום על הסרט בתחילת הפעולה מקביל לנתונים. כשם שפעולת המחשב מתבטאת ע״י העברת נתונים מהזכרון ליחידת העיבוד המרכזית, שינויים והחזרתם לזכרון, כך מתבטאת פעולתה של מכונת טיורינג ע״י קריאת סיפרה במשבצת, שינוייה (אם זה נחוץ) וכתיבת הסיפרה החדשה. כאמור תיארנו מכונת טיורינג שנועדה להוסיף 1 למספר נתון, אבל אפשר כמובן לבנות מכונה שתחבר שני מספרים כלשהם. כללית ניתן לומר שאפשר לבנות מכונת טיורינג שתבצע כל פעולת חישוב שנעלה על דעתנו. יותר מזה, אנשים שונים יכולים לבנות מכונות טיורינג שונות לביצוע אותה פעולה — ולמעשה אפשר לבנות אינסוף מכונות לבצוע כל פעולה ופעולה. כך שבדברנו על מכונות טיורינג אנו מדברים על אינסוף מכונות שונות.15תגליתו הגדולה של טיורינג התבטאה בכך שהיא לא חייבה לעסוק בכל אינסוף המכונות; קיימת מכונה אחת — מכונת טיורינג האוניברסלית — היכולה לבצע את כל מה שמכונת טיורינג אחרת יכולה לבצע. כך, למשל, אם ברצוננו לחבר שני מספרים נכתוב על הסרט את שני המספרים יחד עם תאור מכונת טיורינג המבצעת את פעולת החיבור, ונפעיל את מכונת טיורינג האוניברסלית על הסרט הזה. כאשר תעצר יכיל הסרט את התוצאה. אם ברצוננו להכפיל שני מספרים נכתוב על הסרט את שני המספרים יחד עם תאור מכונת טיורינג המבצעת כפל, ונפעיל את מכונת טיורינג האוניברסלית על הסרט הזה; כשהיא תעצר יכיל הסרט את מכפלת שני המספרים. את תאור המכונות הניתן למכונה האוניברסלית אפשר לעשות על ידי מתן מספר — הקרוי מספר גאדל, על שם המתמטיקאי האוסטרי גאדל. (Gödel) לא נכנס כאן לפרטים כיצד אנו מקבלים מספר זה, אבל נדגיש שמכונת טיורינג האוניברסלית דומה בתאורה לכל מכונת טיורינג אחרת — מכשיר בעל מספר סופי של מצבים הפועל על סרט שבמשבצותיו רשומות ספרות.
אם נשוב להקבלה שערכנו בין מכונות טיורינג למחשבים, הרי שניתן להשוות מכונת טיורינג רגילה למחשב חד־תכליתי, כגון מחשב שנבנה אך ורק לצורך חישוב זוויות ההגבהה של לוע התותח, ואילו מכונת טיורינג האוניברסלית מקבילה למחשב רב־תכליתי, כלומר מחשב היכול לבצע כל הנדרש ממנו בהתאם לאופי התכנית שמזינים לו. כדי להפעיל מחשב רב־תכליתי עלינו להכניס לזכרונו גם את הנתונים שרוצים לעבדם וגם את התכנית המפעילה את המחשב ומדריכה אותו כיצד לעבד את הנתונים הללו. הוא הדין לגבי מכונת טיורינג האוניברסלית. גם כאן, עלינו לכתוב על הסרט את הנתונים ואת תאורה של מכונת טיורינג היכולה לבצע את הפעולה המבוקשת. תאור זה של מכונת טיורינג המסויימת הנו בעצם שווה־ערך לתכנית המחשב.
אם נתבונן ביתר פרוט בפעולת מכונת טיורינג האוניברסלית נגלה תופעה נוספת. כיוון שהמכונה האוניברסלית מקבלת בסרט גם את ה״תכנית״ וגם את הנתונים, ושניהם רשומים באמצעות ספרות, אפשר הדבר שתוך כדי הפעולה ישנה המכשיר את ה״תכנית״. במלים אחרות, מנקודת ראותה של מכונת טיורינג האוניברסלית אין הבדל מהותי בין הנתונים אותם צריכה היא לעבד ובין ה״תכנית״ המדריכה אותה כיצד לעבדם. עובדה זאת הנחתה את ד״ר פון נוימן ואת ד״ר גולדשטיין בבניית המחשב של פרינסטון: על המחשב להיות רב תכליתי. כלומר, פעולה כלשהי שיבצע תישלט ע״י תכנית האגורה בזכרונו ; לא יהיה הבדל עקרוני בין התכנית ובין הנתונים שעל המחשב לעבדם; את שניהם אפשר יהיה לשנות תוך כדי בצוע פעולות החישוב. ואכן, יכולת זאת לשנות את התכנית היא מקור עוצמתם של המחשבים הרב־תכליתיים, המהווים את רובה המכריע של אוכלוסיית המחשבים בעולם.
״מכונת ההבדלים״ (1822) של צ׳רלס באבאז׳ האיש שהגה את העקרונות הלוגיים המאפיינים את המחשבים העכשוויים

בעיות אי־ההכרעה
הקשר בין מחשבים אלקטרוניים ומכונות טיורינג הנו אף חזק יותר ממה שצויין קודם. נדמה לעצמנו מחשב רב תכליתי הפועל ללא הגבלה בסרטים מגנטיים לצורך ביצוע עבודה שהוטלה עליו. מחשב כזה, מבחינת כושר ביצועו, שווה־ערך למכונת טיורינג אוניברסלית. כלומר, כל אשר אפשר לחשב ע״י מכונת טיורינג אוניברסלית אפשר לחשב ע״י מחשב כזה, ולהיפך: כל אשר יכול מחשב כזה לבצע אפשר לבצע ע״י מכונת טיורינג אוניברסלית. צריך רק להדגיש שהשוואה זאת מתייחסת רק לשאלה של מה ניתן לבצע ולא לשאלת יעילות הביצוע. שכן, אלו היינו בונים מחשב שיכולתו מוגבלת רק לביצוע הפעולות הפשוטות שמבצעת מכונת טיורינג אוניברסלית, אזי פעולות המבוצעות כעת בחלקיקי הדקה היו דורשות שנות עבודה של מחשב מעין זה. למרות זאת מאפשר לנו חקר מכונות טיורינג להסיק מסקנות על כושר פעולתם של המחשבים המודרניים והמתוחכמים ביותר. תופעה ידועה למתכנתים היא שלמרות כל מאמציהם משתרבבת לפעמים טעות (bug) בתכנית, בשלה אין היא מבצעת את מה שהמתכנת הועיד לה לעשות. טעות זאת, שעשויה להיות השמטה של הוראה מסויימת או של צעד מסויים בתוך ההוראה, גוזלת זמן יקר לאיתורה ומהווה מטרד רציני בעבודת התיכנות. מכאן ברורה החשיבות שהיתה יכולה להיות לתכנית בודקת, אשר תוזן בתכנית הנבדקת ובתאור התפקיד שעל זו למלא, וכתוצאה מהבדיקה תאמר לנו אם אמנם עשויה התכנית הנבדקת למלא את התפקיד שהועד לה. אולם עד כמה שמשימה זו נשמעת פשוטה, אחת התוצאות המפתיעות שמתקבלות מחקר מכונת טיורינג היא, שאין שום אפשרות לכתוב תכנית בודקת כזאת אשר תוכל לבדוק את כל האפשרויות. כל תכנית בודקת שנכתבה עד עתה או שתיכתב אי פעם — תיכשל במקרים מסויימים, היינו: או שתתעלם מטעויות בתכנית שגויה או ש״תגלה״ שגיאות בתכנית נכונה. ופירושה המעשי של עובדה זאת, בז׳ארגון המקצועי הוא, שלא ניתן לבנות מכונת טיורינג אשר בכל מקרה תכריע אם מכונת16טיורינג מסויימת מחשבת פונקציה נתונה.
מכלול הבעיות הקשורות בשאלה: האם קיימת מכונת טיורינג שיכולה לבצע תפקיד מסויים, נושאת את השם ״בעיות הכרעה״.
הרעיון המרכזי מאחורי הוכחת משפטי אי־ההכרעה הוא, שקיימות מגבלות יסודיות ליכולתה של מכונת טיורינג ״להבין״ את תאור עצמה; ולכן, למשל, אין בנמצא מכונת טיורינג שיכולה לקבוע אם היא עצמה אינה שגויה. בניסוח אחר: אין מחשב יכול ״להבין״ את המודל של עצמו בצורה מעמיקה ולהסיק מכך מסקנות על התנהגות עצמו.
ניקח עתה דוגמא נוספת של בעיית הכרעה. נניח שנתונה תכנית המבצעת את תפקידה ללא טעויות, ומוצעת לנו תכנית אחרת, שטוענים עליה כי בכוחה לא רק להחליף את התכנית המקורית אלא גם לבצע את תפקידה ביעילות גבוהה יותר. האמנם? מתברר שאין אנו יכולים לאמת טענה זאת; ביתר דיוק: אין שום אפשרות לכתוב תכנית שתבדוק עבור כל שתי תכניות אם הן שוות ערך, כלומר שתיתנה תמיד תוצאות זהות אם יזינו אותן בנתונים זהים.
שתי תוצאות תיאורטיות אלה, ותוצאות דומות המתקבלות מתורת מכונות טיורינג, מצביעות על מגבלות יסודיות של המחשבים; עם זאת אין לראות בהן סוף פסוק. מחקר יותר מעמיק המצביע על הסיבה שבעיה זו או אחרת אינה ניתנת להכרעה מאפשר לאתר את התחום המכיל את הפתרון לבעיה, ואף כי אין אפשרות להחליט אם שתי תכניות כלשהן הן שוות ערך, פותחו שיטות אשר במקרים רבים מאפשרות למחשב לעבד תכנית אחת ולמצוא תכנית אחרת, יעילה ממנה, המבצעת את אותו התפקיד עצמו.

אבות הקיברנטיקה, המתמטיקאים נורברט וינר (1894־1964)
וג׳ון פון ניומן (1903־1957)

פתירת בעיות סבוכות
הסיבה לתרומתן הגדולה של מכונות טיורינג לשטח המחשבים היא הצרוף המוצלח של פשטות וכלליות. מצד אחד, כל הצעדים שעושה מכונת טיורינג הינם פשוטים בתכלית: שנוי מצב ותזוזה על הסרט, או כתיבה עליו; מצד שני, כל אשר ניתן להעשות ע״י מחשב גדול — על עושר הפעולות האריתמטיות והלוגיות שלו — אפשר לעשות בעזרת מכונת טיורינג. הפשטות מאפשרת את הפעלת הכלים המתימטיים לחקר מכונות טיורינג, והכלליות מבטיחה שלתוצאות החקר המתימטי תהיינה השלכות מרובות. כפי שהודגש קודם, אין מכונות טיורינג מיצגות את יעילות פעולות המחשב, ולכן התוצאות שהתקבלו מחקר מכונות טיורינג הצביעו על מה שאפשר לבצע באופן עקרוני בעזרת מחשבים ולא על יעילות הבצוע. במשך שנים סברו החוקרים שאין אפשרות להסיק מסקנות מחקר מכונות טיורינג על יעילות החישוב. בשנים האחרונות התברר שאין המצב כך וכי אפשר שחקר שאלות מסוימות הקשורות במכונות טיורינג יצביע על קיום שיטות פתרון מעשיות — שהן הרבה יותר יעילות מכל הידוע כיום. נסיים את המאמר בתאור התפתחות מפתיעה זו.
ידוע הסיפור על ממציא משחק השח־מט, אשר כפרס על המצאתו ביקש מהמלך להניח עבורו גרגיר חיטה על המשבצת הראשונה של לוח השח־מט, שני גרגירים על השניה, ארבעה גרגירים על השלישית, 16 על הרביעית וכן הלאה. ומה רבה היתה הפתעתו של המלך כאשר התברר לו שאין די חיטה באסמיו כדי למלא את בקשתו ״הצנועה״ של הממציא. בעיות דומות לזו, שמספר החישובים הנדרש לפתרונן גדל בטור גיאומטרי, ידועות בייחוד בשטח חקר הביצועים ותיכנות מתימטי. לדוגמא, ״בעיות הסוכן הנוסע״, המציגה את השאלה הבאה: מהו המרחק המינימלי שעל הסוכן לעבור כדי לבקר בכל הערים במדינה. כללית ניתן לומר שכדי להשיב על שאלה זו לגבי עשר ערים נדרשים אלפי צעדי חישוב, לגבי 20 ערים — מיליונים, לגבי 30 ערים — מיליארדים ולגבי 40 ערים נדרשים ביליוני חישובים.
פירושן המעשי של דוגמאות אלו הוא, שאם גם אפשר לפתור בעיה מסויימת תוך מספר שעות במחשב מהיר, הרי סיבוך קטן של הבעיה יאריך את זמן פתרונה לימים, אם לא לשבועות, של זמן המחשב; ולכן אין לחשוב על פתרון מעשי אפילו בעזרת מחשב. יותר מזאת, גם אם נבנה מחשבים גדולים ומהירים פי מאה מהקיימים נוכל לפתור רק בעיות פשוטות למדי מסוג זה. מכאן, חשוב ביותר לדעת אם ניתן למצוא שיטות פתרון לבעיות אלו, שלא ידרשו זמן חישוב הגדל בטור גיאומטרי. וכאן אנו חוזרים לטיורינג; התברר שבאמצעות חקר מכונות טיורינג אפשר למצוא תשובה לשאלה זו, ומשיהיו בידינו שיטות פתרון מהירות נוכל לצפות מהמחשב לפתור עבורנו בעיות כלכליות ארגוניות מורכבות המטרידות אותנו כבר היום.17