סוד הפירמידה
5,000 שנה משמשות שלוש הפירמידות של גיזה מצבת-עד לגאון האדם, אך גם עדות אירונית לכשלונו החרוץ להשיג את הנצח. שלושה פרעונים — סנאפרו, חיאופס (בנו) ו-חופרע (נכדו) — הקימו בזה אחר זה קברים אדירים להגן על גופותיהם החנוטות עד שיקים אותם האל אוזיריס לתחיה. ואכן, יכלו הקברים לאיתני הטבע, אך הגויות נחמסו מתוכם בידי שודדים בטרם חלף דור.
וזה, בעצם, שורש התעלומה: מה טעם מצא חופרע לחזור על איוולת אבותיו — כשכבר נוכח שאין בפירמידה שום מגן? שנית, מדוע לא ניסה, כמותם, להסתיר את הכניסה לחדר קבורתו ע״י מבוך מעברים ומסדרונות? ושלישית, היכן גופתו של חופרע?
שאלות אלו הביאו שודדים וארכיאולוגים כאחד למחשבה, שקברו הגלוי של הופרע אינו אלא מסווה לקברו האמיתי — המצוי אי-שם בינות ל-2,300,000 גושי אבן אדירים, שמשקל כל אחד מהם מגיע עד 15 טון.
האמנם? על שאלה זאת עתיד להשיב מחשב י.ב.מ. 1130, שהוטס במיוחד למצריים, לאחר שיפענח ״צלום רנטגן״ של הפירמידה.
כידוע, מופצץ כדור הארץ ע״י מטר חלקיקים — מואונים — הנוצרים מהתנגשות בין הקרינה הקוסמית לאטמוספירה. בשל מהירותם הגבוהה מצליחים מואונים רבים לחדור את קירות הפירמידה (מכל הכיוונים) ולהגיע אל מרכזה, בעוד אחרים נעצרים בדרך. ככל שהדרך אטומה יותר כן קטן מספר המואונים שיגיע אל מרכז הפירמידה. מכאן, מספר המואונים המגיע למרכז מכל כיוון עשוי לגלות אם מצוי בכיוון זה חלל ריק — דוגמת אולם קבורה נסתר.
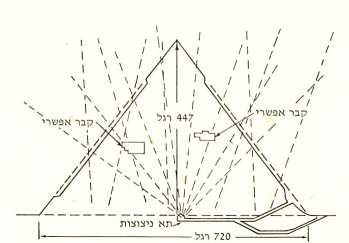
המדענים הציבו באולם הרחב שבבסיס הפירמידה שני תאי-ניצוצות הקולטים את המואונים, בעוד קאורדינטות הפגיעה מועברים לסרטים מגנטיים. לאחר ששלושה מיליון מסלולים של מואונים יירשמו על 80 גלילי סרטים מגנטיים, יתנו למחשב למפות את הקאורדינטות ולמנות את מספר המואונים שהגיעו בכל אחד מהכיוונים הנתונים. מצויידים בנתוני הצפיפות ינסו המדענים לאתר סוף-סוף את מקום קבורתו הסודי של חופרע. כל זה בתנאי שלא יקרה משהו בלתי צפוי: קללת הפרעונים.

אמנות ממוחשבת 1968
הירחון האמריקאי Computer and Automation פירסם לאחרונה את התמונות הזוכות בתחרות האמנות הממוחשבת לשנת 1968.
בפרס הראשון זכתה יצירה צבעונית בשם ״יונק הדבש״, פרי עבודתם של שני מתכנתים, קארי סטראנד וגארי קראיגמיל. הציור פותח בעזרת בעיה מתימטית הידועה בשם ״שלושת החיפושיות״ (Three Bug Problem).
היינו: כל אחת משלוש חיפושיות, הניצבות בקודקודיו של משולש נתון, נעה לעבר החיפושית שמימינה ורושמת אגב-כך את מסלול תנועתה. הציור הסופי הוא תוצאה של חזרה משולשת של הבעיה. כאשר נתיביה של כל אחת מהן הודפסה בצבע שונה.